题目内容
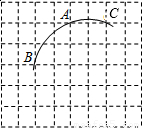
 如图,一圆弧过方格的格点A、B、C,试在方格中建立平面直角坐标系,使点A的坐标为(2,3),则该圆弧所在圆的圆心坐标是
如图,一圆弧过方格的格点A、B、C,试在方格中建立平面直角坐标系,使点A的坐标为(2,3),则该圆弧所在圆的圆心坐标是
- A.(-1,1)
- B.(2,1)
- C.(1,1)
- D.(1,0)
D
分析:连接AC,作出AB、AC的垂直平分线,其交点即为圆心.
解答: 解:如图所示,
解:如图所示,
连接AC,作出AB、AC的垂直平分线,其交点即为圆心.
∵点A的坐标为(2,3),
∴该圆弧所在圆的圆心坐标是(1,0).
故选:D.
点评:此题主要考查了垂径定理的应用,根据线段垂直平分线上的点到这条线段两端点的距离相等,找到圆的半径,半径的交点即为圆心是解题关键.
分析:连接AC,作出AB、AC的垂直平分线,其交点即为圆心.
解答:
 解:如图所示,
解:如图所示,连接AC,作出AB、AC的垂直平分线,其交点即为圆心.
∵点A的坐标为(2,3),
∴该圆弧所在圆的圆心坐标是(1,0).
故选:D.
点评:此题主要考查了垂径定理的应用,根据线段垂直平分线上的点到这条线段两端点的距离相等,找到圆的半径,半径的交点即为圆心是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
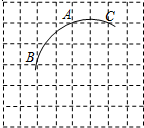 13、如图,一圆弧过方格的格点A、B、C,以每个方格子为单位长度过,试在方格中建立适当的平面直角坐标系,则该圆弧所在圆的圆心坐标是
13、如图,一圆弧过方格的格点A、B、C,以每个方格子为单位长度过,试在方格中建立适当的平面直角坐标系,则该圆弧所在圆的圆心坐标是
 (2011•成华区二模)如图,一圆弧过方格的格点A、B、C,在方格中建立平面直角坐标系,使点A的坐标为(-1,3),则该圆弧所在圆的圆心坐标是
(2011•成华区二模)如图,一圆弧过方格的格点A、B、C,在方格中建立平面直角坐标系,使点A的坐标为(-1,3),则该圆弧所在圆的圆心坐标是 如图,一圆弧过方格的格点A、B、C,试在方格中建立平面直角坐标系,使点A的坐标为(2,3),则该圆弧所在圆的圆心坐标是( )
如图,一圆弧过方格的格点A、B、C,试在方格中建立平面直角坐标系,使点A的坐标为(2,3),则该圆弧所在圆的圆心坐标是( )