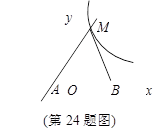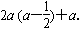Question

（11·柳州）（本题满分6分）．

     如图，一次函数y＝－4x－4的图象与x轴、y轴分别交于A、C

（1）求抛物线的函数表达式；

（2）设抛物线的顶点为D，求四边形ABDC的面积；

（3）作直线MN平行于x轴，分别交线段AC、BC于点M、N．问在x轴上是否存在点P，使得△PMN是等腰直角三角形？如果存在，求出所有满足条件的P点的坐标；如果不存在，请说明理由．

 

Answer 1

【答案】

（1）∵一次函数y＝－4x－4的图象与x轴、y轴分别交于A、C两点，

∴A (－1，0)  C (0，－4)

把A (－1，0)  C (0，－4)代入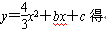

S_△ECA＝×2×4＝4

S_{四边形ABDC}＝S_△EDB－S_△ECA＝12

（3）抛物线的对称轴为x＝－1

做BC的垂直平分线交抛物线于E，交对称轴于点D₃

易求AB的解析式为y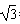＝－x＋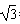

∵D₃E是BC的垂直平分线

∴D₃E∥AB

设D₃E的解析式为y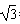＝－x＋b

∵D₃E交x轴于（－1，0）代入解析式得b＝－,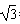

∴y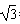＝－x－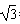

把x＝－1代入得y＝0

∴D₃ (－1，0),

【解析】略