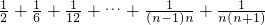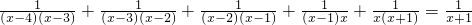题目内容
阅读理解题:
(1)观察各式:
=
=
-
,
=
=
-
,
=
=
-
,
=
=
-
,
=
=
-
,…
(2)请利用上述规律计算(要求写出计算过程):
+
+
+…+
+
解:原式=
(3)请利用上述规律,解方程:
+
+
+
+
=
解:原方程可变形如下:
(1)观察各式:
| 1 |
| 2 |
| 1 |
| 1×2 |
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 12 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 20 |
| 1 |
| 4×5 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 30 |
| 1 |
| 5×6 |
| 1 |
| 5 |
| 1 |
| 6 |
(2)请利用上述规律计算(要求写出计算过程):
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| (n-1)n |
| 1 |
| n(n+1) |
解:原式=
(3)请利用上述规律,解方程:
| 1 |
| (x-4)(x-3) |
| 1 |
| (x-3)(x-2) |
| 1 |
| (x-2)(x-1) |
| 1 |
| (x-1)x |
| 1 |
| x(x+1) |
| 1 |
| x+1 |
解:原方程可变形如下:
分析:(2)根据(1)中的等量关系可得:
=
-
,可把(2)中的式子分解,再相加即可;
(3)根据(1)中的规律,可把方程左边分解,再相加可达到化简的目的.
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
(3)根据(1)中的规律,可把方程左边分解,再相加可达到化简的目的.
解答:解:(2)原式=1-
+
-
+…+
-
+
-
=1-
=
;
(3)原方程可变为
-
+
-
+…+
-
=
,
即
-
=
,
∴
=
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
=
| n |
| n+1 |
(3)原方程可变为
| 1 |
| x-4 |
| 1 |
| x-3 |
| 1 |
| x-3 |
| 1 |
| x-2 |
| 1 |
| x |
| 1 |
| x+1 |
| 1 |
| x+1 |
即
| 1 |
| x-4 |
| 1 |
| x+1 |
| 1 |
| x+1 |
∴
| 1 |
| x-4 |
| 2 |
| x+1 |
点评:本题考查了分式的混合运算,解题的关键是找出规律,即相差1的两个数或式子乘积分之一等于较小数或式子分之一减去较大数或式子分之一.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
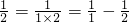 ,
, ,
, ,
, ,
, ,…
,…