题目内容
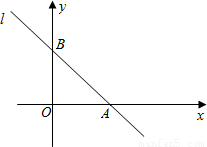
（2010•镇江）在直角坐标系xOy中，直线l过（1，3）和（3，1）两点，且与x轴，y轴分别交于A，B两点．（1）求直线l的函数关系式；
（2）求△AOB的面积．
【答案】分析：（1）把两点坐标代入函数解析式得到关于k、b的二元一次方程组并求解即可得到函数解析式；
（2）求出直线与坐标轴的交点，代入三角形面积公式即可．
解答：解：（1）设直线l的函数关系式为y=kx+b（k≠0），
把（3，1），（1，3）代入①得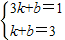
，
解方程组得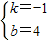
，
∴直线l的函数关系式为y=-x+4；
（2）当x=0时，y=4，∴B（0，4），
当y=0，-x+4=0，
解得x=4，
∴A（4，0），
∴S△AOB=
AO•BO=
×4×4=8．
点评：本题主要考查待定系数法求函数解析式，在平面直角坐标系中求三角形的面积，找出点的坐标或边的长度是解题的关键．
（2）求出直线与坐标轴的交点，代入三角形面积公式即可．
解答：解：（1）设直线l的函数关系式为y=kx+b（k≠0），
把（3，1），（1，3）代入①得
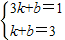，解方程组得
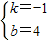，∴直线l的函数关系式为y=-x+4；
（2）当x=0时，y=4，∴B（0，4），
当y=0，-x+4=0，
解得x=4，
∴A（4，0），
∴S△AOB=
AO•BO=×4×4=8．点评：本题主要考查待定系数法求函数解析式，在平面直角坐标系中求三角形的面积，找出点的坐标或边的长度是解题的关键．
练习册系列答案
相关题目
