��Ŀ����
���������ĸ��60�����գ�С����С����С������Ҫ�ڹ���ǰϦ�����ĸ����������5������������İ���֮�顣С��˵����������һ����ѧ�⣺�Ѽ�5����������������3���ˣ�ÿ������1�����ж����ַ��䷽��?��С��������˵��������˵�����Ϊx��y��z�������г�����x+y+z=4����С�½���˵������ô����ͳ�������������м����������⡣����������˵˵�������������������ĸ�����( )
| A��7�� | B��6�� | C��5�� | D��3�� |
B
x+y+z=5��
��1����x=1ʱ��y=2��z=2��y=3��z=1��y=1��z=3��
��2����y=1ʱ��x=2��z=2��x=3��z=1��x=1��z=3��
��3����z=1ʱ��x=2��y=2��x=3��y=1��x=1��y=3��
�������������������ĸ�����6����ѡB��
��1����x=1ʱ��y=2��z=2��y=3��z=1��y=1��z=3��
��2����y=1ʱ��x=2��z=2��x=3��z=1��x=1��z=3��
��3����z=1ʱ��x=2��y=2��x=3��y=1��x=1��y=3��
�������������������ĸ�����6����ѡB��

��ϰ��ϵ�д�
�����Ŀ



 �Ľ⼯�ǣ� ��
�Ľ⼯�ǣ� ��



 (3)x=y (4��
(3)x=y (4�� ��5��2xy-3=0
��5��2xy-3=0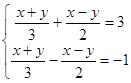
 �Ƿ���
�Ƿ��� �Ľ⣬��
�Ľ⣬�� ��
��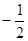 ��b=1
��b=1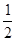 ��b=
��b=