题目内容
 已知:如图,△ABO与△BCD都是等边三角形,O为坐标原点,点B、D在x轴上,AO=2,点A、C在一反比例函数图象上.
已知:如图,△ABO与△BCD都是等边三角形,O为坐标原点,点B、D在x轴上,AO=2,点A、C在一反比例函数图象上.(1)求此反比例函数解析式;
(2)求点C的坐标;
(3)问:以点A为顶点,且经过点C的抛物线是否经过点(0,
| ||
| 2 |
分析:(1)首先过点A、C分别作AF⊥OB于点F,CE⊥DB于点E,根据AO=2,△ABO与△BCD是等边三角形,得出A点坐标,进而求出反比例函数解析式;
(2)首先表示出C点坐标,进而代入函数解析式求出即可;
(3)首先设y=a(x+1)2+
,把点C坐标代入得出a的值,进而将点(0,
)得出答案.
(2)首先表示出C点坐标,进而代入函数解析式求出即可;
(3)首先设y=a(x+1)2+
| 3 |
| ||
| 2 |
解答: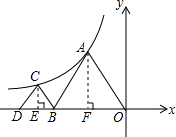 解:(1)过点A、C分别作AF⊥OB于点F,CE⊥DB于点E,
解:(1)过点A、C分别作AF⊥OB于点F,CE⊥DB于点E,
∵AO=2,△ABO与△BCD是等边三角形,
∴OF=1,FA=
,
∴点A的坐标是(-1,
),
把(-1,
)代入y=
,
得k=-
,
∴反比例函数的解析式是y=
;
(2)设BE=a,则CE=
a
∴点C的坐标是(-2-a,
a),
把点C的坐标代入y=
得(-2-a)
a=-
,
a=
-1,
∴点C的坐标是(-1-
,
-
);
(3)点C的抛物线是经过点(0,
).
理由:设y=a(x+1)2+
,
把点C坐标代入得a=
,
∴y=
(x+1)2+
,
当x=0时,代入上式得y=
,
∴点C的抛物线是经过点(0,
).
 解:(1)过点A、C分别作AF⊥OB于点F,CE⊥DB于点E,
解:(1)过点A、C分别作AF⊥OB于点F,CE⊥DB于点E,∵AO=2,△ABO与△BCD是等边三角形,
∴OF=1,FA=
| 3 |
∴点A的坐标是(-1,
| 3 |
把(-1,
| 3 |
| k |
| x |
得k=-
| 3 |
∴反比例函数的解析式是y=
-
| ||
| x |
(2)设BE=a,则CE=
| 3 |
∴点C的坐标是(-2-a,
| 3 |
把点C的坐标代入y=
-
| ||
| x |
得(-2-a)
| 3 |
| 3 |
a=
| 2 |
∴点C的坐标是(-1-
| 2 |
| 6 |
| 3 |
(3)点C的抛物线是经过点(0,
| ||
| 2 |
理由:设y=a(x+1)2+
| 3 |
把点C坐标代入得a=
| ||||
| 2 |
∴y=
| ||||
| 2 |
| 3 |
当x=0时,代入上式得y=
| ||
| 2 |
∴点C的抛物线是经过点(0,
| ||
| 2 |
点评:此题主要考查了反比例函数的综合应用以及图象上点的坐标特点等知识,根据已知表示出C点坐标是解题关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 图象分别交于点C、D,CE⊥x轴于点E,
图象分别交于点C、D,CE⊥x轴于点E,
 已知:如图,△ABO与△BCD都是等边三角形,O为坐标原点,点B、D在x轴上,AO=2,点A、C在一反比例函数图象上.
已知:如图,△ABO与△BCD都是等边三角形,O为坐标原点,点B、D在x轴上,AO=2,点A、C在一反比例函数图象上.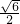 )?请说明理由.
)?请说明理由.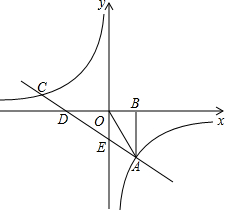 已知,如图,△ABO的顶点A是双曲线
已知,如图,△ABO的顶点A是双曲线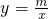 与直线y=kx+b在第四象限内的交点,AB⊥x轴于点B,OA=
与直线y=kx+b在第四象限内的交点,AB⊥x轴于点B,OA=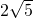 ,tan∠OAB=
,tan∠OAB= .另一交点为C(-8,n).求:
.另一交点为C(-8,n).求: