题目内容
在△ABC中,若tanA=1,sinB= ,你认为最确切的判断是( )
,你认为最确切的判断是( )A.△ABC是等腰三角形
B.△ABC是等腰直角三角形
C.△ABC是直角三角形
D.△ABC是一般锐角三角形
【答案】分析:先根据特殊角的三角函数值求出∠A,∠B的值,再根据三角形内角和定理求出∠C即可判断.
解答:解:∵tanA=1,sinB=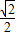 ,
,
∴∠A=45°,∠B=45°.
又∵三角形内角和为180°,
∴∠C=90°.
∴△ABC是等腰直角三角形.
故选B.
点评:解答此题的关键是熟记特殊角的三角函数值,三角形内角和定理及等腰三角形的判定.
解答:解:∵tanA=1,sinB=
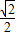 ,
,∴∠A=45°,∠B=45°.
又∵三角形内角和为180°,
∴∠C=90°.
∴△ABC是等腰直角三角形.
故选B.
点评:解答此题的关键是熟记特殊角的三角函数值,三角形内角和定理及等腰三角形的判定.

练习册系列答案
相关题目