题目内容
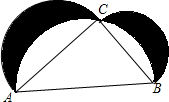 教材八年级上册数学第43页的阅读材料中提到公元前约400年,古希腊的希波克拉底研究了他自己所画的图形,如图所示,他得出了两个月牙形(图中阴影部分)的面积之和的一个结论.如果你能解决下面这个问题,那说明你也知道希波克拉底得出的结论了.这个图形是以Rt△ACB的三条边为直径做半圆得到的,若直角边AC=5,BC=3,那么两个月牙形(图中阴影部分)的面积之和等于
教材八年级上册数学第43页的阅读材料中提到公元前约400年,古希腊的希波克拉底研究了他自己所画的图形,如图所示,他得出了两个月牙形(图中阴影部分)的面积之和的一个结论.如果你能解决下面这个问题,那说明你也知道希波克拉底得出的结论了.这个图形是以Rt△ACB的三条边为直径做半圆得到的,若直角边AC=5,BC=3,那么两个月牙形(图中阴影部分)的面积之和等于分析:两个月牙形(图中阴影部分)的面积之和等于以AC和BC为直径的两个半圆面积之和再减去以AB为直径的半圆面积与三角形ABC的面积之差,经整理得图中阴影部分的面积之和等于三角形ABC的面积.
解答:解:∵AC=5,BC=3,
∴AB=
,
∴
AC=
,
BC=
∴以AC和BC为直径的两个半圆面积之和为
+
=4.25π,
∴以AB为直径的半圆面积与三角形ABC的面积之差为
-
=
-7.5;
∴两个月牙形(图中阴影部分)的面积之和等于4.25π-(
π-7.5)=7.5+0.25π.
故答案为:7.5.
∴AB=
| 34 |
∴
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴以AC和BC为直径的两个半圆面积之和为
π(
| ||
| 2 |
π(
| ||
| 2 |
∴以AB为直径的半圆面积与三角形ABC的面积之差为
π(
| ||
| 2 |
| 3×5 |
| 2 |
| 17π |
| 4 |
∴两个月牙形(图中阴影部分)的面积之和等于4.25π-(
| 17 |
| 4 |
故答案为:7.5.
点评:本题考查了扇形面积的计算,得出阴影部分的面积是解此题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目