题目内容
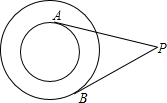 两个同心圆,PA切小圆于点A,PB切大圆于B,PA=3cm,PB=2cm,则两圆所围成的圆环面积是
两个同心圆,PA切小圆于点A,PB切大圆于B,PA=3cm,PB=2cm,则两圆所围成的圆环面积是
- A.1cm2
- B.5cm2
- C.πcm2
- D.5πcm2
D
分析:连接OP、OA、OB,设OA=r,OB=R,求出圆环的面积是πR2-πr2=π(R2-r2),由切线性质得出∠OAP=∠OBP=90°,由勾股定理得出OP2=OA2+PA2=OB2+PB2,求出R2-r2=5,代入求出即可.
解答:
连接OP、OA、OB,设OA=r,OB=R,
则圆环的面积是πR2-πr2=π(R2-r2),
∵两个同心圆,PA切小圆于点A,PB切大圆于B,
∴∠OAP=∠OBP=90°,
由勾股定理得:OP2=OA2+PA2=OB2+PB2,
∴32+r2=R2+22,
∴R2-r2=5,
∴圆环的面积是πR2-πr2=π(R2-r2)=5π(cm2),
故选D.
点评:本题考查了切线的性质,勾股定理的应用,关键是得出圆环的面积是πR2-πr2=π(R2-r2)和求出R2-r2的值.
分析:连接OP、OA、OB,设OA=r,OB=R,求出圆环的面积是πR2-πr2=π(R2-r2),由切线性质得出∠OAP=∠OBP=90°,由勾股定理得出OP2=OA2+PA2=OB2+PB2,求出R2-r2=5,代入求出即可.
解答:

连接OP、OA、OB,设OA=r,OB=R,
则圆环的面积是πR2-πr2=π(R2-r2),
∵两个同心圆,PA切小圆于点A,PB切大圆于B,
∴∠OAP=∠OBP=90°,
由勾股定理得:OP2=OA2+PA2=OB2+PB2,
∴32+r2=R2+22,
∴R2-r2=5,
∴圆环的面积是πR2-πr2=π(R2-r2)=5π(cm2),
故选D.
点评:本题考查了切线的性质,勾股定理的应用,关键是得出圆环的面积是πR2-πr2=π(R2-r2)和求出R2-r2的值.

练习册系列答案
相关题目