题目内容
已知正方形的四个顶点坐标为(1、2),(3、2),(1、4),(3、4),若二次函数y=ax2的图象与正方形有交点,则a的取值范围是
≤a≤4
≤a≤4.
| 2 |
| 9 |
| 2 |
| 9 |
分析:作出图形,根据二次函数的增减性,当x=1时,函数值不大于正方形左上角顶点的纵坐标,当x=3时,函数值不小于正方形右下角的顶点的纵坐标,分别列出不等式求解即可.
解答: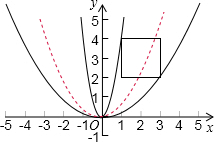 解:如图,∵正方形的四个顶点坐标为(1,2),(3,2),(1,4),(3,4),
解:如图,∵正方形的四个顶点坐标为(1,2),(3,2),(1,4),(3,4),
∴要使二次函数y=ax2的图象与正方形有交点,
则当x=1时,a×12≤4,解得a≤4,
当x=3时,a×32≥2,解得a≥
,
∴
≤a≤4.
故答案为:
≤a≤4.
 解:如图,∵正方形的四个顶点坐标为(1,2),(3,2),(1,4),(3,4),
解:如图,∵正方形的四个顶点坐标为(1,2),(3,2),(1,4),(3,4),∴要使二次函数y=ax2的图象与正方形有交点,
则当x=1时,a×12≤4,解得a≤4,
当x=3时,a×32≥2,解得a≥
| 2 |
| 9 |
∴
| 2 |
| 9 |
故答案为:
| 2 |
| 9 |
点评:本题考查了二次函数的性质,根据二次函数的增减性列出不等式是解题的关键,作出图形更形象直观.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目