题目内容
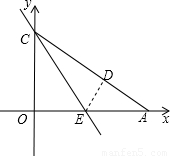
(2005•沈阳)如图,Rt△OAC是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点C在y轴上,OC=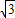 ,∠CAO=30度.将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
,∠CAO=30度.将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.(1)求折痕CE所在直线的解析式;
(2)求点D的坐标;
(3)设点M为直线CE上的一点,过点M作AC的平行线,交y轴于点N,是否存在这样的点M,使得以M、N、D、C为顶点的四边形是平行四边形?若存在,请求出符合条件的点M的坐标;若不存在,请说明理由.
【答案】分析:(1)因为∠CAO=30°,由折叠可知∠OCE=∠ECD= ∠OCA=30°,
∠OCA=30°,
在Rt△COE中,利用三角函数可求OE=OC•tan∠OCE=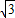 ×
×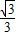 =1,从而可求点E的坐标是(1,0).
=1,从而可求点E的坐标是(1,0).
因为OC=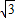 ,所以C(0,
,所以C(0,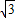 ).
).
可设直线CE的解析式为y=kx+b,将C、E的坐标代入,可得到关于k、b的方程组,解之即可;
(2)在Rt△AOC中,利用三角函数可求出AC、AO的值,因为CD=OC=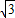 ,可求出AD=AC-CD=2
,可求出AD=AC-CD=2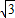 -
-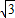 =
=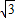 .
.
要求D的坐标,需过点D作DF⊥OA于点F.
在Rt△AFD中,利用三角函数可求DF=AD•sin∠CAO=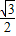 ,AF=AD•cos∠CAO=
,AF=AD•cos∠CAO= ,所以OF=AO-AF=
,所以OF=AO-AF= ,从而点D的坐标是(
,从而点D的坐标是( ,
,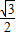 );
);
(3)需分情况讨论:
第一种情况:若此点在第四象限内,可设其为M1,延长DF交直线CE于M1,连接M1O,则有DM1∥y轴.
因为OF= ,所以可设点M1的坐标为(
,所以可设点M1的坐标为( ,y1),利用点M1在直线CE上,可得y1的值,即可求出点M1的坐标是(
,y1),利用点M1在直线CE上,可得y1的值,即可求出点M1的坐标是( ,-
,-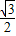 ),所以有DM1=DF+FM1=
),所以有DM1=DF+FM1=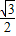 +
+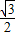 =
=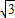 ,OC=
,OC=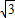 ,所以DM1=OC.
,所以DM1=OC.
利用一组对边平行且相等的四边形是平行四边形可知四边形CDM1O为平行四边形.而点O在y轴上,所以点M1是符合条件的点.
第二种情况:此点在第二象限内,设为M2.可过点D作DN∥CE交y轴于N,过N点作NM2∥CD交直线CE于点M2,则四边形M2NDC为平行四边形.
利用平行四边形的对边分别相等,可知M2N=CD=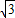 ,
,
又因M2N∥CD,DN∥CE,所以∠NM2C=∠ACE,∠OCE=∠M2CN,CN=M2N.
又因M2N=CD=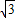 ,所以CN=
,所以CN=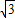 .
.
接着可作M2H⊥y轴于点H,利用两直线平行,内错角相等可得∠M2NC=∠NCD,∴∠M2NH=∠OCA=60°.
在Rt△M2NH中,利用三角函数可求出M2H,NH的值,利用HO=HN+CN+OC=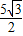 可得M2(-
可得M2(- ,
,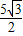 ).
).
解答:解:(1)由题意知∠CAO=30°,
∴∠OCE=∠ECD= ∠OCA=30°,
∠OCA=30°,
∴在Rt△COE中,OE=OC•tan∠OCE=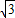 ×
× =1,
=1,
∴点E的坐标是(1,0),
设直线CE的解析式为y=kx+b.
把点C(0,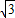 ),E(1,0)代入得
),E(1,0)代入得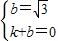 ,
,
∴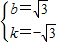 ,
,
∴直线CE的解析式为y=-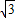 x+
x+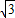 .
.
(2)在Rt△AOC中,AC=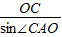 =2
=2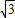 ,
,
AO=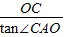 =3,
=3,
∵CD=OC=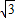 ,
,
∴AD=AC-CD=2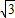 -
-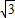 =
=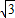 ,
,
过点D作DF⊥OA于点F,
在Rt△AFD中,DF=AD•sin∠CAO=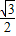 ,
,
AF=AD•cos∠CAO= ,
,
∴OF=AO-AF= .
.
∴点D的坐标是( ,
, ).
).
(3)存在两个符合条件的M点,
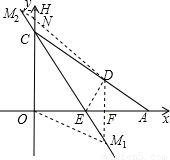 第一种情况:此点在第四象限内,设为M1,延长DF交直线CE于M1,
第一种情况:此点在第四象限内,设为M1,延长DF交直线CE于M1,
连接M1O,M1O∥AC,
则有DM1∥y轴,
∵OF= ,
,
∴设点M1的坐标为( ,y1),
,y1),
又∵点M1在直线CE上,
∴将点M1的坐标代入y=-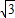 x+
x+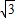 中,
中,
得y1=-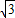 ×
× +
+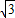 =-
=-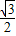 ,即FM1=
,即FM1=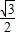 .
.
∴点M1的坐标是( ,-
,-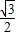 ),
),
又∵DM1=DF+FM1=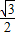 +
+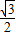 =
=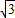 ,OC=
,OC= ,
,
∴DM1=OC,
又∵DM1∥OC,
∴四边形CDM1O为平行四边形,
又∵点O在y轴上,
∴点M1是符合条件的点.
第二种情况:此点在第二象限内,设为M2,
过点D作DN∥CE交y轴于N,过N点作NM2∥CD交直线CE于点M2,
则四边形M2NDC为平行四边形,
∴M2N=CD=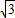 ,
,
∵M2N∥CD,DN∥CE,
∴∠NM2C=∠ACE,∠OCE=∠M2CN,
∴CN=M2N,
∵M2N=CD=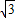 ,
,
∴CN=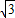 ,
,
作M2H⊥y轴于点H,
∵M2N∥CD,
∴∠M2NC=∠NCD,
∴∠M2NH=∠OCA=60°,
在Rt△M2NH中,
M2H=M2N•sin60°=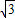 ×
×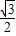 =
= ,
,
NH=M2N•cos60°=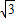 ×
× =
=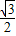 ,
,
∴HO=HN+CN+OC=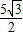 ,
,
∴M2(- ,
,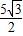 ),
),
∴点M2是符合条件的点,
综上所述,符合条件的两个点的坐标分别为M1( ,-
,-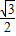 ),M2(-
),M2(- ,
,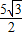 ).
).
点评:本题的解决需要综合运用待定系数法、三角函数等知识,另外解决这类问题常用到分类讨论、数形结合、方程和转化等数学思想方法.
 ∠OCA=30°,
∠OCA=30°,在Rt△COE中,利用三角函数可求OE=OC•tan∠OCE=
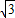 ×
×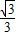 =1,从而可求点E的坐标是(1,0).
=1,从而可求点E的坐标是(1,0).因为OC=
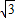 ,所以C(0,
,所以C(0,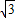 ).
).可设直线CE的解析式为y=kx+b,将C、E的坐标代入,可得到关于k、b的方程组,解之即可;
(2)在Rt△AOC中,利用三角函数可求出AC、AO的值,因为CD=OC=
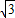 ,可求出AD=AC-CD=2
,可求出AD=AC-CD=2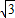 -
-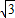 =
=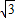 .
.要求D的坐标,需过点D作DF⊥OA于点F.
在Rt△AFD中,利用三角函数可求DF=AD•sin∠CAO=
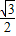 ,AF=AD•cos∠CAO=
,AF=AD•cos∠CAO= ,所以OF=AO-AF=
,所以OF=AO-AF= ,从而点D的坐标是(
,从而点D的坐标是( ,
,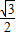 );
);(3)需分情况讨论:
第一种情况:若此点在第四象限内,可设其为M1,延长DF交直线CE于M1,连接M1O,则有DM1∥y轴.
因为OF=
 ,所以可设点M1的坐标为(
,所以可设点M1的坐标为( ,y1),利用点M1在直线CE上,可得y1的值,即可求出点M1的坐标是(
,y1),利用点M1在直线CE上,可得y1的值,即可求出点M1的坐标是( ,-
,-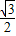 ),所以有DM1=DF+FM1=
),所以有DM1=DF+FM1=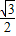 +
+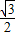 =
=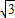 ,OC=
,OC=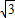 ,所以DM1=OC.
,所以DM1=OC.利用一组对边平行且相等的四边形是平行四边形可知四边形CDM1O为平行四边形.而点O在y轴上,所以点M1是符合条件的点.
第二种情况:此点在第二象限内,设为M2.可过点D作DN∥CE交y轴于N,过N点作NM2∥CD交直线CE于点M2,则四边形M2NDC为平行四边形.
利用平行四边形的对边分别相等,可知M2N=CD=
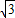 ,
,又因M2N∥CD,DN∥CE,所以∠NM2C=∠ACE,∠OCE=∠M2CN,CN=M2N.
又因M2N=CD=
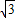 ,所以CN=
,所以CN=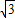 .
.接着可作M2H⊥y轴于点H,利用两直线平行,内错角相等可得∠M2NC=∠NCD,∴∠M2NH=∠OCA=60°.
在Rt△M2NH中,利用三角函数可求出M2H,NH的值,利用HO=HN+CN+OC=
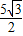 可得M2(-
可得M2(- ,
,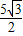 ).
).解答:解:(1)由题意知∠CAO=30°,
∴∠OCE=∠ECD=
 ∠OCA=30°,
∠OCA=30°,∴在Rt△COE中,OE=OC•tan∠OCE=
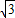 ×
× =1,
=1,∴点E的坐标是(1,0),
设直线CE的解析式为y=kx+b.
把点C(0,
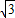 ),E(1,0)代入得
),E(1,0)代入得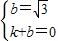 ,
,∴
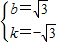 ,
,∴直线CE的解析式为y=-
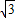 x+
x+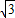 .
.(2)在Rt△AOC中,AC=
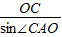 =2
=2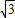 ,
,AO=
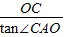 =3,
=3,∵CD=OC=
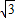 ,
,∴AD=AC-CD=2
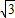 -
-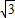 =
=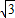 ,
,过点D作DF⊥OA于点F,
在Rt△AFD中,DF=AD•sin∠CAO=
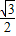 ,
,AF=AD•cos∠CAO=
 ,
,∴OF=AO-AF=
 .
.∴点D的坐标是(
 ,
,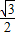 ).
).(3)存在两个符合条件的M点,
 第一种情况:此点在第四象限内,设为M1,延长DF交直线CE于M1,
第一种情况:此点在第四象限内,设为M1,延长DF交直线CE于M1,连接M1O,M1O∥AC,
则有DM1∥y轴,
∵OF=
 ,
,∴设点M1的坐标为(
 ,y1),
,y1),又∵点M1在直线CE上,
∴将点M1的坐标代入y=-
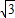 x+
x+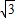 中,
中,得y1=-
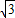 ×
× +
+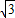 =-
=-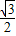 ,即FM1=
,即FM1=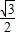 .
.∴点M1的坐标是(
 ,-
,-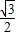 ),
),又∵DM1=DF+FM1=
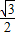 +
+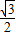 =
=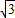 ,OC=
,OC= ,
,∴DM1=OC,
又∵DM1∥OC,
∴四边形CDM1O为平行四边形,
又∵点O在y轴上,
∴点M1是符合条件的点.
第二种情况:此点在第二象限内,设为M2,
过点D作DN∥CE交y轴于N,过N点作NM2∥CD交直线CE于点M2,
则四边形M2NDC为平行四边形,
∴M2N=CD=
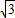 ,
,∵M2N∥CD,DN∥CE,
∴∠NM2C=∠ACE,∠OCE=∠M2CN,
∴CN=M2N,
∵M2N=CD=
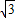 ,
,∴CN=
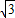 ,
,作M2H⊥y轴于点H,
∵M2N∥CD,
∴∠M2NC=∠NCD,
∴∠M2NH=∠OCA=60°,
在Rt△M2NH中,
M2H=M2N•sin60°=
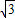 ×
×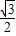 =
= ,
,NH=M2N•cos60°=
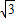 ×
× =
=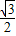 ,
,∴HO=HN+CN+OC=
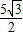 ,
,∴M2(-
 ,
,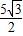 ),
),∴点M2是符合条件的点,
综上所述,符合条件的两个点的坐标分别为M1(
 ,-
,-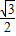 ),M2(-
),M2(- ,
,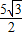 ).
).点评:本题的解决需要综合运用待定系数法、三角函数等知识,另外解决这类问题常用到分类讨论、数形结合、方程和转化等数学思想方法.

练习册系列答案
相关题目
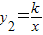 (x<0)分别交于点C、D,且C点的坐标为(-1,2).
(x<0)分别交于点C、D,且C点的坐标为(-1,2).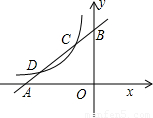
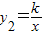 (x<0)分别交于点C、D,且C点的坐标为(-1,2).
(x<0)分别交于点C、D,且C点的坐标为(-1,2).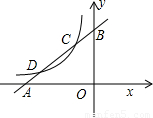
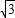 ,∠CAO=30度.将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
,∠CAO=30度.将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.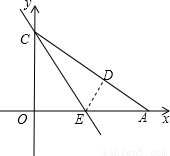
 (x<0)分别交于点C、D,且C点的坐标为(-1,2).
(x<0)分别交于点C、D,且C点的坐标为(-1,2).