题目内容
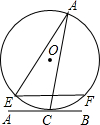 如图,直线AB与半径为1的⊙O相切于点C,D是⊙O上一点,且∠EDC=22.5°,弦EF∥AB,则EF的长度为( )
如图,直线AB与半径为1的⊙O相切于点C,D是⊙O上一点,且∠EDC=22.5°,弦EF∥AB,则EF的长度为( )| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
分析:作辅助线,连接OC与OE.根据一条弧所对的圆周角等于它所对的圆心角的一半,可知∠EOC的度数;再根据切线的性质定理,圆的切线垂直于经过切点的半径,可知OC⊥AB;又由EF∥AB,可知OC⊥EF,最后由勾股定理可将EF的长求出.
解答: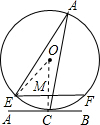 解:连接OE和OC,且OC与EF的交点为M.
解:连接OE和OC,且OC与EF的交点为M.
∵∠EDC=22.5°,
∴∠COE=45°.
∵AB与⊙O相切,
∴OC⊥AB,
又∵EF∥AB,
∴OC⊥EF,即△EOM为直角三角形.
在Rt△EOM中,EM=sin45°×OE=
×1=
,
∵EF=2EM,
∴EF=
.
故选B.
 解:连接OE和OC,且OC与EF的交点为M.
解:连接OE和OC,且OC与EF的交点为M.∵∠EDC=22.5°,
∴∠COE=45°.
∵AB与⊙O相切,
∴OC⊥AB,
又∵EF∥AB,
∴OC⊥EF,即△EOM为直角三角形.
在Rt△EOM中,EM=sin45°×OE=
| ||
| 2 |
| ||
| 2 |
∵EF=2EM,
∴EF=
| 2 |
故选B.
点评:本题主要考查切线的性质及直角三角形的勾股定理.难度不大,关键是正确地构造直角三角形.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
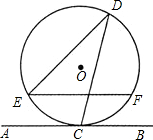 如图,直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长度为( )
如图,直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长度为( )| A、2 | ||
B、2
| ||
C、
| ||
D、2
|
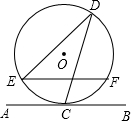 如图,直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长度为
如图,直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长度为 如图,直线AB与半径为5的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长度为
如图,直线AB与半径为5的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长度为