Question

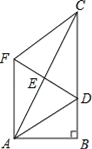
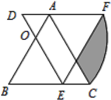
【题目】如图，已知在四边形ABCD中，AD∥BC，∠ABC＝90°，以AB为直径的⊙O交边DC于E、F两点，AD＝1，BC＝5，设⊙O的半径长为r．

（1）联结OF，当OF∥BC时，求⊙O的半径长；

（2）过点O作OH⊥EF，垂足为点H，设OH＝y，试用r的代数式表示y；

（3）设点G为DC的中点，联结OG、OD，△ODG是否能成为等腰三角形？如果能，试求出r的值；如不能，试说明理由．

Answer 1

【答案】(1)3；(2)y=；(3)△ODG能成为等腰三角形，r=2

【解析】

(1)证OF为梯形ABCD的中位线，得出r=OF=(AD+BC)=3即可；

(2)连接OD、OC，过点D作DM⊥BC于M，则CM=BC﹣BM=4，由勾股定理得出DC=2，由四边形ABCD的面积=△DOC的面积+△AOD的面积+△BOC的面积，进而得出答案；

(3)证OG是梯形ABCD的中位线，得出OG∥AD，OG=3，DG=CD=，由勾股定理得OD=，分三种情况，分别求解即可．

解：(1)∵OF∥BC，OA=OB，

∴OF为梯形ABCD的中位线，

∴OF=(AD+BC)=(1+5)=3，

即⊙O的半径长为3；

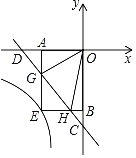
(2)连接OD、OC，过点D作DM⊥BC于M，如图1所示：

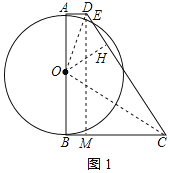
∵AD∥BC，∠ABC=90°，且DM⊥BC，

∴四边形ABMD为矩形，

则BM=AD=1，

∴CM=BC﹣BM=4，

∴DC=，

∵四边形ABCD的面积=△DOC的面积+△AOD的面积+△BOC的面积，

∴(1+5)×2r=×2×y+r×1+r×5，

整理得：y=；

(3)△ODG能成为等腰三角形，理由如下：

∵点G为DC的中点，OA=OB，

∴OG是梯形ABCD的中位线，

∴OG∥AD，OG=(AD+BC)=(1+5)=3，

DG=CD=，

由勾股定理得：OD=，

分三种情况：

①DG=DO时，则，无解；

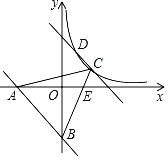
②OD=OG时，如图2所示：

，

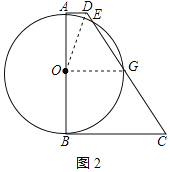
解得：；

③GD=GO时，作OH⊥CD于H，如图3所示：

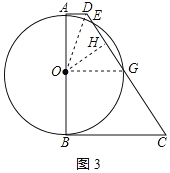
∠GOD=∠GDO，

∵OG∥AD，

∴∠ADO=∠GOD，

∴∠ADO=∠GDO，

∴DO是∠ADG的平分线，

由题意知：OA⊥AD，

又OH⊥CD，

∴OA=OH，

则此时圆O和CD相切，不合题意；

综上所述，△ODG能成为等腰三角形，r=．