题目内容
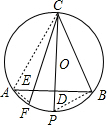
 如图,已知在⊙O中,CD过圆心O交⊙O于点P,作AB⊥CD,垂足为D,过点C任作一条弦CF交AB于点E.
如图,已知在⊙O中,CD过圆心O交⊙O于点P,作AB⊥CD,垂足为D,过点C任作一条弦CF交AB于点E.
(1)求证:CB2=CE•CF;
(2)连接BP,若BD:CD=2:3,求sin∠BPD的值.
 (1)证明:连接AC、AF,
(1)证明:连接AC、AF,∵CD过圆心,且AB⊥CD,
∴AC=BC,
∴∠CAE=∠F,
又∵∠ACE=∠ACF,
∴△ACE∽△FCA,
∴
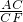 =
=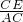 ,
,即AC2=CE.CF,
∴CB2=CE.CF;
(2)解:连接BP,
∵CP是⊙O直径,
∴∠CBP=90°,
∵BD⊥CP,
∴∠BPD=∠CBD,
∵BD:CD=2:3,
设BD=2k,CD=3k,
在Rt△BCD中,BC=
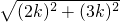 =
= ,
,∴sin∠CBD=
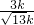 =
=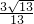 =sin∠BPD.
=sin∠BPD.分析:(1)连接AC、AF,根据已知条件,易证△ACE∽△FCA,所以
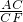 =
=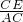 ,即AC2=CE.CF.
,即AC2=CE.CF.(2)连接BP,因为BD:CD=2:3,设BD=2k,CD=3k,在Rt△BCD中,BC=
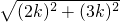 =
= ,所以sin∠CBD=
,所以sin∠CBD=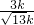 =
=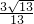 =sin∠BPD.
=sin∠BPD.点评:本题主要考查了三角形的相似的判定和性质,题目典型,是一个大综合题,难度较大,有利于培养同学们的钻研精神和坚韧不拔的意志品质.

练习册系列答案
相关题目
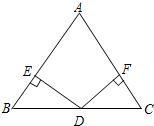 20、如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
20、如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.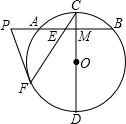 作⊙O的切线交BA的延长线于点P.
作⊙O的切线交BA的延长线于点P.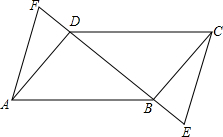 (2011•普宁市一模)如图,已知在?ABCD中,E、F是对角线BD延长线上的两点,且∠BCE=∠DAF,求证:△ECD≌△FAB.
(2011•普宁市一模)如图,已知在?ABCD中,E、F是对角线BD延长线上的两点,且∠BCE=∠DAF,求证:△ECD≌△FAB.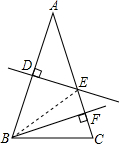 如图,已知在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,求∠A的度数.
如图,已知在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,求∠A的度数.