题目内容
(2013•吉安模拟)如图,P是?ABCD的边AD上一点,将△ABP与△DCP沿PB与PC翻折得到△EPB和△FPC,PA与PD翻折后落在同一直线上.若△PAB的面积为4,PD=2PA,则△PBC的面积为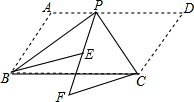
12
12
.
分析:根据等高的三角形的面积的比等于底边的比求出△PCD的面积,再根据平行四边形与三角形的面积的关系解答.
解答:解:在平行四边形ABCD中,AD=BC,AD∥BC,
∵△PAB的面积为4,PD=2PA,
∴△PCD的面积=2×4=8,
设AD、BC间的距离为h,
则S△PAB+S△PCD=
(PA+PD)h=
AD•h,
S△PBC=
BC•h,
∴S△PBC=4+8=12.
故答案为:12.
∵△PAB的面积为4,PD=2PA,
∴△PCD的面积=2×4=8,
设AD、BC间的距离为h,
则S△PAB+S△PCD=
| 1 |
| 2 |
| 1 |
| 2 |
S△PBC=
| 1 |
| 2 |
∴S△PBC=4+8=12.
故答案为:12.
点评:本题考查了翻折的性质,平行四边形的对边平行且相等的性质,等高的三角形的面积的比等于底边的比,熟记性质并求出△PCD的面积是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•吉安模拟)已知圆锥如图所示放置,其主视图面积为12,俯视图的周长为6n,则该圆锥的侧面积为
(2013•吉安模拟)已知圆锥如图所示放置,其主视图面积为12,俯视图的周长为6n,则该圆锥的侧面积为