题目内容
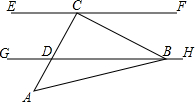如图，直线EF∥GH，在等腰Rt△ABC中，AC=BC=| 3 |
分析：先在Rt△BCD中利用正切函数计算出∠CBD=30°，则∠CDB=60°，然后利用平行线的性质求解．
解答：解：∵BC=
，CD=1，∠ACB=90°，
∴tan∠CBD=
=
=
，
∴∠CBD=30°，
∴∠CDB=60°，
∵EF∥GH，
∴∠ACE=∠CDB=60°．
故答案为60°．
| 3 |
∴tan∠CBD=
| CD |
| BC |
| 1 | ||
|
| ||
| 3 |
∴∠CBD=30°，
∴∠CDB=60°，
∵EF∥GH，
∴∠ACE=∠CDB=60°．
故答案为60°．
点评：本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．也考查了平行线的性质．
练习册系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
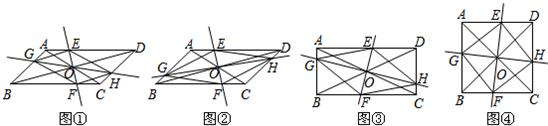
在 ABCD中，AC、BD交于点O，过点O作直线EF、GH，分别交平行四边形的四条边于E、G、F、H四点，连结EG、GF、FH、HE.
在 ABCD中，AC、BD交于点O，过点O作直线EF、GH，分别交平行四边形的四条边于E、G、F、H四点，连结EG、GF、FH、HE.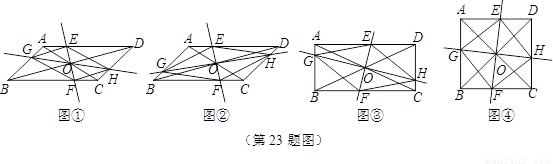
如图，直线EF∥GH，在等腰Rt△ABC中，AC=BC=
，∠ACB=90°，顶点C、B分别在直线EF、GH上，AC与直线GH交于点D．若测得CD=1，则∠ACE=________．