题目内容
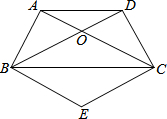已知：如图，在等腰梯形ABCD中，AD∥BC，对角线AC与BD交于O点，分别过B、C作AC、BD的平行线，交点为E．①试判断四边形OBEC的形状，并证明你的结论；
②对角线AC、BD满足什么条件时，四边形OBEC是正方形？
分析：①先根据AC∥BE，BD∥CE，证出四边形OBEC是平行四边形，再根据四边形ABCD是等腰梯形，证出OB=OC，即可得出四边形OBEC是菱形；
②根据正方形的判定即可得出答案．
②根据正方形的判定即可得出答案．
解答：解：①∵AC∥BE，BD∥CE，
∴四边形OBEC是平行四边形，
∵四边形ABCD是等腰梯形，
∴AC=BD，AB=CD，∠ABC=∠DCB，
∴△ABC≌△DCB，
∴∠ACB=∠DBC，
∴OB=OC，
∴四边形OBEC是菱形；
②当AC、BD满足互相垂直的条件时，四边形OBEC是正方形．
∴四边形OBEC是平行四边形，
∵四边形ABCD是等腰梯形，
∴AC=BD，AB=CD，∠ABC=∠DCB，
∴△ABC≌△DCB，
∴∠ACB=∠DBC，
∴OB=OC，
∴四边形OBEC是菱形；
②当AC、BD满足互相垂直的条件时，四边形OBEC是正方形．
点评：此题考查了等腰梯形的性质，用到的知识点是菱形、全等三角形的判定、等腰梯形的性质，关键是综合应用有关性质．
练习册系列答案
相关题目
