题目内容
(2008•无锡)已知抛物线y=ax2-2x+c与它的对称轴相交于点A(1,-4),与y轴交于C,与x轴正半轴交于B.(1)求这条抛物线的函数关系式;
(2)设直线AC交x轴于D,P是线段AD上一动点(P点异于A,D),过P作PE∥x轴交直线AB于E,过E作EF⊥x轴于F,求当四边形OPEF的面积等于
 时点P的坐标.
时点P的坐标.
【答案】分析:(1)由题意可知抛物线的顶点就是A点,因此可将A的坐标代入抛物线的解析式中,并根据对称轴x=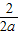 =1,联立方程组即可求出a,c的值,进而可得出抛物线的解析式.
=1,联立方程组即可求出a,c的值,进而可得出抛物线的解析式.
(2)四边形OPEF是个直角梯形,可先求出AD,AB所在直线的解析式,根据AD所在直线的解析式设出P的坐标,又由于PE∥x轴,P、E两点的纵坐标相同,然后根据AB所在直线的解析式得出E点的坐标,进而可求出F点的坐标.根据求出的P、E、F三点坐标,可得出梯形的上下底OF、EP的长以及直角梯形的高EF的长(即E点纵坐标的绝对值),根据梯形的面积公式即可得出关于梯形的面积与P点坐标的函数解析式,然后将S= 代入函数中即可求出P点的坐标.
代入函数中即可求出P点的坐标.
解答: 解:(1)由题意,知点A(1,-4)是抛物线的顶点,
解:(1)由题意,知点A(1,-4)是抛物线的顶点,
∴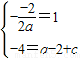
∴a=1,c=-3,
∴抛物线的函数关系式为y=x2-2x-3.
(2)由(1)知,点C的坐标是(0,-3).
设直线AC的函数关系式为y=kx+b,
则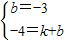
∴b=-3,k=-1,
∴y=-x-3.
由y=x2-2x-3=0,得x1=-1,x2=3,
∴点B的坐标是(3,0).
设直线AB的函数关系式是y=mx+n,
则 解得m=2,n=-6.
解得m=2,n=-6.
∴直线AB的函数关系式是y=2x-6.
设P点坐标为(xP,yP),则yP=-xP-3.
∵PE∥x轴,
∴E点的纵坐标也是-xP-3.
设E点坐标为(xE,yE),
∵点E在直线AB上,
∴-xP-3=2xE-6,
∴xE=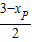 .
.
∵EF⊥x轴,
∴F点的坐标为(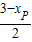 ,0),
,0),
∴PE=xE-xP=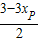 ,OF=
,OF=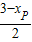 ,EF=-(-xP-3)=xP+3,
,EF=-(-xP-3)=xP+3,
∴S四边形OPEF= (PE+OF)•EF=
(PE+OF)•EF= (
(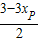 +
+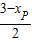 )•(xP+3)=
)•(xP+3)= ,
,
2xP2+3xP-2=0,
∴xP=-2,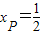 ,
,
当y=0时,x=-3,
而-3<-2<1,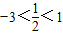 ,
,
∴P点坐标为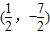 和(-2,-1)
和(-2,-1)
点评:本题着重考查了待定系数法求二次函数解析式及二次函数的综合应用.
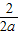 =1,联立方程组即可求出a,c的值,进而可得出抛物线的解析式.
=1,联立方程组即可求出a,c的值,进而可得出抛物线的解析式.(2)四边形OPEF是个直角梯形,可先求出AD,AB所在直线的解析式,根据AD所在直线的解析式设出P的坐标,又由于PE∥x轴,P、E两点的纵坐标相同,然后根据AB所在直线的解析式得出E点的坐标,进而可求出F点的坐标.根据求出的P、E、F三点坐标,可得出梯形的上下底OF、EP的长以及直角梯形的高EF的长(即E点纵坐标的绝对值),根据梯形的面积公式即可得出关于梯形的面积与P点坐标的函数解析式,然后将S=
 代入函数中即可求出P点的坐标.
代入函数中即可求出P点的坐标.解答:
 解:(1)由题意,知点A(1,-4)是抛物线的顶点,
解:(1)由题意,知点A(1,-4)是抛物线的顶点,∴
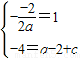
∴a=1,c=-3,
∴抛物线的函数关系式为y=x2-2x-3.
(2)由(1)知,点C的坐标是(0,-3).
设直线AC的函数关系式为y=kx+b,
则
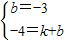
∴b=-3,k=-1,
∴y=-x-3.
由y=x2-2x-3=0,得x1=-1,x2=3,
∴点B的坐标是(3,0).
设直线AB的函数关系式是y=mx+n,
则
 解得m=2,n=-6.
解得m=2,n=-6.∴直线AB的函数关系式是y=2x-6.
设P点坐标为(xP,yP),则yP=-xP-3.
∵PE∥x轴,
∴E点的纵坐标也是-xP-3.
设E点坐标为(xE,yE),
∵点E在直线AB上,
∴-xP-3=2xE-6,
∴xE=
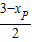 .
.∵EF⊥x轴,
∴F点的坐标为(
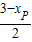 ,0),
,0),∴PE=xE-xP=
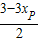 ,OF=
,OF=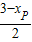 ,EF=-(-xP-3)=xP+3,
,EF=-(-xP-3)=xP+3,∴S四边形OPEF=
 (PE+OF)•EF=
(PE+OF)•EF= (
(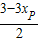 +
+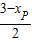 )•(xP+3)=
)•(xP+3)= ,
,2xP2+3xP-2=0,
∴xP=-2,
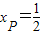 ,
,当y=0时,x=-3,
而-3<-2<1,
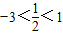 ,
,∴P点坐标为
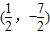 和(-2,-1)
和(-2,-1)点评:本题着重考查了待定系数法求二次函数解析式及二次函数的综合应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 时点P的坐标.
时点P的坐标.