题目内容
如图，在周长为20cm的平行四边形ABCD中，AB≠AD，AC，BD相交于点O，OE⊥BD交AD于E，求△ABE的周长．分析：利用平行四边形、等腰三角形的性质，将△ABE的周长转化为平行四边形的边长之间的和差关系．
解答：解：∵四边形ABCD是平行四边形，
∴AC、BD互相平分，
∴O是BD的中点．
又∵OE⊥BD，
∴OE为线段BD的中垂线，
∴BE=DE．
又∵△ABE的周长=AB+AE+BE，
∴△ABE的周长=AB+AE+DE=AB+AD．
又∵□ABCD 的周长为20cm，
∴AB+AD=10cm
∴△ABE的周长=10cm．
∴AC、BD互相平分，
∴O是BD的中点．
又∵OE⊥BD，
∴OE为线段BD的中垂线，
∴BE=DE．
又∵△ABE的周长=AB+AE+BE，
∴△ABE的周长=AB+AE+DE=AB+AD．
又∵□ABCD 的周长为20cm，
∴AB+AD=10cm
∴△ABE的周长=10cm．
点评：本题考查了平行四边形的性质．平行四边形的对角线互相平分．
练习册系列答案
相关题目
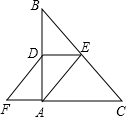如图，在Rt△ABC中，∠BAC=90°，D、E分别是AB、BC的中点，F在CA延长线上，∠FDA=∠B，AC=6，AB=8，则四边形AEDF的周长为（ ）
7、如图，在?ABCD中，BD为对角线，点E、O、F分别是AB、BD、BC的中点，且OE=3，OF=2，则?ABCD的周长是（ ）
（2012•内江）如图，在矩形ABCD中，AB=10，BC=5，点E、F分别在AB、CD上，将矩形ABCD沿EF折叠，使点A、D分别落在矩形ABCD外部的点A1、D1处，则阴影部分图形的周长为（ ）
如图，在Rt△ABC中，∠BAC=90°，D、E分别是AB、BC的中点，F在CA延长线上，∠FDA=∠B，AC=6，AB=8，则四边形AEDF的周长为