题目内容
2008年5月12日,我国四川汶川发生了8.0级的特大地震,给汶川人民的生命财产带来巨大损失.地震发生后,我市人民积极响应党中央号召支援灾区,迅速募捐了大量的药品、食品、帐篷等救灾物资,计划首批用某运输公司的20辆汽车运送200吨上述三种物资到地震灾区,每辆车只能装运同一种物资且必须装满.根据下表提供的信息,解答下列问题.| 物资名称 | 药品 | 食品 | 帐篷 |
| 每辆车运载量(吨) | 8 | 10 | 12 |
| 每吨货物运输所用费用(百元) | 8 | 7 | 6 |
(2)如果装运每种物资的车辆数都多于4辆,那么车辆安排方案有几种写出每种安排安案;
(3)若要使此次运输费W(百元)最小,应采用哪种方案,并求出最少运费.
【答案】分析:(1)根据题意可知:总重量=药品车辆×单位载药量+食品车辆×单位载食品量+帐篷车辆×单位载帐篷量.可得到函数式;
(2)再根据题意可得到二元一次不等式,解出x的取值范围,就可以得到所需的所有方案;
(3)根据题意可得到w的关于x的解析式,根据解析式可求出最低运费.
解答:解:(1)根据题意,装运药品的车辆数为x,装运食品的车辆数为y,那么装运帐篷的车辆数为(20-x-y),(1分)
则有8x+10y+12(20-x-y)=200,
整理,得y=20-2x;(2分)
(2)由(1)知,装运药品、食品、帐篷的车辆数分别为x,20-2x,20-x-y,
由题意,得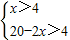 解不等式组,得4<x<8,
解不等式组,得4<x<8,
因为x为整数,所以x的值为5,6,7,(2分)
所以安排方案有3种:
方案一:装运药品5车,食品10车,帐篷5车;
方案二:装运药品6车,食品8车,帐篷6车;
方案三:装运药品7车,食品6车,帐篷7车.(3分)
(3)W=8x×8+10(20-2x)×7+12x×6=-4x+1400,(1分)
因为-4<0,所以W的值随x的增大而减小,
要使费用W最小,则x=7,故选方案三,
W最小=-4×7+1400=1372(百元).(2分)
答:当装运药品7车、食品6车、帐篷7车时费用最低,最低费用为1372百元.(1分)
点评:此题利用了:总重量=药品车辆×单位载药量+食品车辆×单位载食品量+帐篷车辆×单位载帐篷量,以及解二元一次不等式的知识和一次函数的性质,k<0,y随x的增大而减小.
(2)再根据题意可得到二元一次不等式,解出x的取值范围,就可以得到所需的所有方案;
(3)根据题意可得到w的关于x的解析式,根据解析式可求出最低运费.
解答:解:(1)根据题意,装运药品的车辆数为x,装运食品的车辆数为y,那么装运帐篷的车辆数为(20-x-y),(1分)
则有8x+10y+12(20-x-y)=200,
整理,得y=20-2x;(2分)
(2)由(1)知,装运药品、食品、帐篷的车辆数分别为x,20-2x,20-x-y,
由题意,得
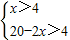 解不等式组,得4<x<8,
解不等式组,得4<x<8,因为x为整数,所以x的值为5,6,7,(2分)
所以安排方案有3种:
方案一:装运药品5车,食品10车,帐篷5车;
方案二:装运药品6车,食品8车,帐篷6车;
方案三:装运药品7车,食品6车,帐篷7车.(3分)
(3)W=8x×8+10(20-2x)×7+12x×6=-4x+1400,(1分)
因为-4<0,所以W的值随x的增大而减小,
要使费用W最小,则x=7,故选方案三,
W最小=-4×7+1400=1372(百元).(2分)
答:当装运药品7车、食品6车、帐篷7车时费用最低,最低费用为1372百元.(1分)
点评:此题利用了:总重量=药品车辆×单位载药量+食品车辆×单位载食品量+帐篷车辆×单位载帐篷量,以及解二元一次不等式的知识和一次函数的性质,k<0,y随x的增大而减小.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 自从2008年5月12日我国四川地区发生特大地震以来,全国人民“众志成城 抗震救灾”,纷纷捐款献爱心,在某校的一次捐款活动中,九年级(1)班30名学生捐款情况如下表:
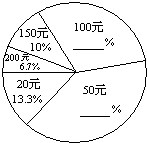
自从2008年5月12日我国四川地区发生特大地震以来,全国人民“众志成城 抗震救灾”,纷纷捐款献爱心,在某校的一次捐款活动中,九年级(1)班30名学生捐款情况如下表:| 捐款(单位:元) | 20 | 50 | 100 | 150 | 200 |
| 人数 | 4 | 12 | 9 | 3 | 2 |
(2)补全右图所示的捐款人数比例的扇形统计图;
(3)请你根据以上信息发表自己的一个见解.
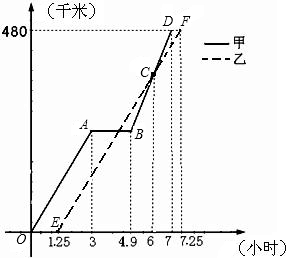 示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:
示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题: