题目内容
第30届奥林匹克运动会在英国伦敦举行．有甲、乙两种价格的奥运会门票，甲种门票价格为4000元人民币/张，乙种门票价格为3000元人民币/张，王老师购买这两种价格的奥运会门票共6张，花了20000元人民币，求甲、乙两种门票各多少张？
分析：先设甲种门票x张，则乙种门票6-x张，根据甲种门票价格为4000元人民币/张，乙种门票价格为3000元人民币/张，花了20000元人民币，列出方程，求出x的值即可．
解答：解：设甲种门票x张，根据题意得：
4000x+3000（6-x）=20000，
解得x=2，
6-2=4（张）；
答：甲、乙两种门票各2张和4张．
4000x+3000（6-x）=20000，
解得x=2，
6-2=4（张）；
答：甲、乙两种门票各2张和4张．
点评：此题考查了一元一次方程的应用，关键是读懂题意，找出题目中的等量关系，根据等量关系列出方程．
练习册系列答案
阅读快车系列答案
相关题目
2008年8月8日，第29届奥林匹克运动会在北京举行，某中学举行了一次“迎奥运知识竞赛”，共有800名学生参加了这次竞赛，为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分）进行统计，请你根据下面尚未完成的频率分布表和频率分布直方图，解答下列问题：
| 8分组 | 频数 | 频率 |
| 50.5～60.5 | 2 | 0.08 |
| 60.5～70.5 | 4 | 0.16 |
| 70.5～80.5 | 5 | 0.20 |
| 80.5～90.5 | 8 | 0.32 |
| 90.5～100 | ||
| 合计 |
（2）补全频率分布直方图；
（3）若成绩在90分以上（不含90分）为优秀，则该校成绩优秀的约为多少人？
2008年8月8日，第29届奥林匹克运动会在北京举行，某中学举行了一次“迎奥运知识竞赛”，共有800名学生参加了这次竞赛，为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分）进行统计，请你根据下面尚未完成的频率分布表和频率分布直方图，解答下列问题：
（1）填充频率分布表中的空格；
（2）补全频率分布直方图；
（3）若成绩在90分以上（不含90分）为优秀，则该校成绩优秀的约为多少人？
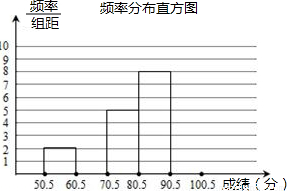
| 8分组 | 频数 | 频率 |
| 50.5～60.5 | 2 | 0.08 |
| 60.5～70.5 | 4 | 0.16 |
| 70.5～80.5 | 5 | 0.20 |
| 80.5～90.5 | 8 | 0.32 |
| 90.5～100 | ||
| 合计 |
（2）补全频率分布直方图；
（3）若成绩在90分以上（不含90分）为优秀，则该校成绩优秀的约为多少人？