题目内容
【题目】函数是描述客观世界运动变化的重要模型,理解函数的本质是重要的任务。
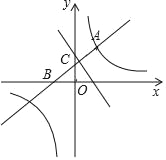
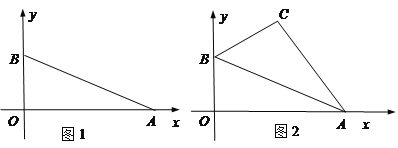
(1)如图1,在平面直角坐标系中,已知点A、B的坐标分别为A(6,0)、B(0,2),点C(x,y)在线段AB上,计算(x+y)的最大值。小明的想法是:这里有两个变量x、y,若最大值存在,设最大值为m,则有函数关系式y=-x+m,由一次函数的图像可知,当该直线与y轴交点最高时,就是m的最大值,(x+y)的最大值为 ;
(2)请你用(1)中小明的想法解决下面问题:
如图2,以(1)中的AB为斜边在右上方作Rt△ABM.设点M坐标为(x,y),求(x+y)的最大值是多少?
【答案】(1)6(2)4+2![]()
【解析】分析:(1)根据一次函数的性质即可得到结论;
(2)根据以AB为斜边在右上方作Rt△ABC,可知点C在以AB为直径的⊙D上运动,根据点C坐标为(x,y),可构造新的函数x+y=m,则函数与y轴交点最高处即为x+y的最大值,此时,直线y=﹣x+m与⊙D相切,再根据圆心点D的坐标,可得C的坐标为(3+![]() ,1+
,1+![]() ),代入直线y=﹣x+m,可得m=4+2
),代入直线y=﹣x+m,可得m=4+2![]() ,即可得出x+y的最大值为4+2
,即可得出x+y的最大值为4+2![]() .
.
详解:(1)6;
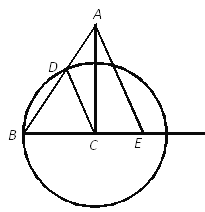
(2)由题可得,点C在以AB为直径的⊙D上运动,点C坐标为(x,y),可构造新的函数x+y=m,则函数与y轴交点最高处即为x+y的最大值,此时,直线y=﹣x+m与⊙D相切,交x轴与E,如图所示,连接OD,CD.
∵A(6,0)、B(0,2),∴D(3,1),∴OD=![]() =
=![]() ,∴CD=
,∴CD=![]() .
.
根据CD⊥EF可得,C、D之间水平方向的距离为![]() ,铅垂方向的距离为
,铅垂方向的距离为![]() ,∴C(3+
,∴C(3+![]() ,1+
,1+![]() ),代入直线y=﹣x+m,可得:1+
),代入直线y=﹣x+m,可得:1+![]() =﹣(3+
=﹣(3+![]() )+m,解得:m=4+2
)+m,解得:m=4+2![]() ,∴x+y的最大值为4+2
,∴x+y的最大值为4+2![]() .故答案为:4+2
.故答案为:4+2![]() .
.


练习册系列答案
相关题目