题目内容
已知:如图,抛物线y=
| ||
| 3 |
| 3 |
(1)直接写出a的值;
(2)在抛物线的对称轴上是否存在一点P,使得⊙P与y轴和直线BC同时相切?若存在,求出点P的坐标,若不存在,请说明理由;
(3)把抛物线沿x轴向右平移m(m>0)个单位,所得抛物线与x轴交于A′、B′两点,
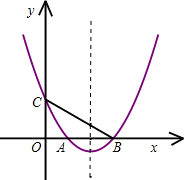 与原抛物线交于点M,当△MA′B′的面积为
与原抛物线交于点M,当△MA′B′的面积为
| ||
| 6 |
分析:(1)把C的坐标代入函数解析式即可求得a的值;
(2)首先求得抛物线的对称轴是x=2,⊙P与y轴和直线BC同时相切,则圆心到直线的距离等于2,然后分P在x轴上方与x轴下方两种情况进行讨论,利用三角函数即可求解;
(3)根据平移的性质可得:A′B′=AB=2,作MN⊥x轴,垂足为N,根据△MA′B′的计算方法,即可求得m的值.
(2)首先求得抛物线的对称轴是x=2,⊙P与y轴和直线BC同时相切,则圆心到直线的距离等于2,然后分P在x轴上方与x轴下方两种情况进行讨论,利用三角函数即可求解;
(3)根据平移的性质可得:A′B′=AB=2,作MN⊥x轴,垂足为N,根据△MA′B′的计算方法,即可求得m的值.
解答: 解:(1)a=3(3分)
解:(1)a=3(3分)
(2)抛物线的对称轴为直线x=2,抛物线与x轴的交点为H A(1,0)B(3,0)(4分)
设P(2,y)作PD⊥BC,垂足为D,作PE⊥y轴,垂足为E,则PD=PE=2
∴当P在x轴上方时
∵tan∠CBO=
=
∴∠CBO=30°(5分) GH=
∴∠PGD=60°
∴PG=y-
=
=
PH=
(6分)
当P在x轴下方时PH=
(7分)
∴P的坐标为(2,
)或(2,-
) (8分)
(3)作MN⊥x轴,垂足为N 由平移可知,A′B′=AB=2
∵△MA′B′的面积为
∴MN=
(9分)
当y=
时,
x2-
x+
=
(10分)
∴x=
∴m=
-
=
(11分)
当y=-
时,
x2-
x+
=-
(12分)
∴x=
∴m=
-
=
(13分)
∴m的值为
或
 解:(1)a=3(3分)
解:(1)a=3(3分)(2)抛物线的对称轴为直线x=2,抛物线与x轴的交点为H A(1,0)B(3,0)(4分)
设P(2,y)作PD⊥BC,垂足为D,作PE⊥y轴,垂足为E,则PD=PE=2
∴当P在x轴上方时
∵tan∠CBO=
| OC |
| OB |
| ||
| 3 |
| ||
| 3 |
∴PG=y-
| ||
| 3 |
| PD |
| sin60° |
4
| ||
| 3 |
5
| ||
| 3 |
当P在x轴下方时PH=
| 3 |
∴P的坐标为(2,
5
| ||
| 3 |
| 3 |
(3)作MN⊥x轴,垂足为N 由平移可知,A′B′=AB=2
∵△MA′B′的面积为
| ||
| 6 |
| ||
| 6 |
当y=
| ||
| 6 |
| ||
| 3 |
4
| ||
| 3 |
| 3 |
| ||
| 6 |
∴x=
4±
| ||
| 2 |
4+
| ||
| 2 |
4-
| ||
| 2 |
| 6 |
当y=-
| ||
| 6 |
| ||
| 3 |
4
| ||
| 3 |
| 3 |
| ||
| 6 |
∴x=
4±
| ||
| 2 |
4+
| ||
| 2 |
4-
| ||
| 2 |
| 2 |
∴m的值为
| 6 |
| 2 |
点评:本题是二次函数的综合题型,其中涉及到的知识点有抛物线的顶点公式和三角形的面积求法.在求有关动点问题时要注意分析题意分情况讨论结果.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
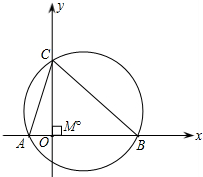 与y轴交点C的纵坐标为3,△ABC的外接圆的圆心为点M.
与y轴交点C的纵坐标为3,△ABC的外接圆的圆心为点M.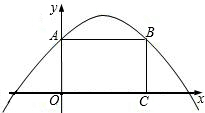 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12,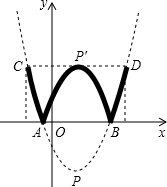 (2013•宁化县质检)已知:如图,抛物线y=ax2+bx+c与x轴交于点A(
(2013•宁化县质检)已知:如图,抛物线y=ax2+bx+c与x轴交于点A(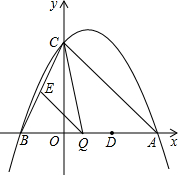 已知,如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A,B,点A的坐标为(4,0).
已知,如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A,B,点A的坐标为(4,0).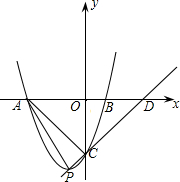 已知,如图,抛物线y=x2+px+q与x轴相交于A、B两点,与y轴交于点C,且OA≠OB,OA=OC,设抛物线的顶点为点P,直线PC与x轴的交点D恰好与点A关于y轴对称.
已知,如图,抛物线y=x2+px+q与x轴相交于A、B两点,与y轴交于点C,且OA≠OB,OA=OC,设抛物线的顶点为点P,直线PC与x轴的交点D恰好与点A关于y轴对称.