题目内容
(2010•攀枝花)如图所示,有三种不透明的卡片,除正面写有不同数字外,其它均相同.将这三张卡片背面朝上洗匀后,第一次随机抽一张,并把这张卡片标有的数字记作一次函数表达式中的k,放回洗匀后,第二次再随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的b.(1)写出k为负数的概率.
(2)求一次函数y=kx+b的图象经过第二,三,四象限的概率(用树状图或列表法求解.)

【答案】分析:(1)列举出所有情况,看k为负数的情况占总情况的多少即可;
(2)列举出所有情况,看k<0,b<0的情况占总情况的多少即可.
解答:解:(1)共有3个数,负数有2个,那么k为负数的概率为: ;
;
(2)列表得共有9种情况,k<0,b<0的共有4种情况,也就是经过第二,三,四象限的共有4种情况,所以概率是 .
.
点评:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)= ,注意本题是放回实验;经过二三四象限的一次函数的k<0,b<0.
,注意本题是放回实验;经过二三四象限的一次函数的k<0,b<0.
(2)列举出所有情况,看k<0,b<0的情况占总情况的多少即可.
解答:解:(1)共有3个数,负数有2个,那么k为负数的概率为:
 ;
;(2)列表得共有9种情况,k<0,b<0的共有4种情况,也就是经过第二,三,四象限的共有4种情况,所以概率是
 .
.
点评:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
 ,注意本题是放回实验;经过二三四象限的一次函数的k<0,b<0.
,注意本题是放回实验;经过二三四象限的一次函数的k<0,b<0. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 x与抛物线y=ax2+b(a≠0)交于A(-4,-2),B(6,3)两点.抛物线与y轴的交点为C.
x与抛物线y=ax2+b(a≠0)交于A(-4,-2),B(6,3)两点.抛物线与y轴的交点为C. ?若存在,试求出此时点P的坐标;若不存在,请说明理由.
?若存在,试求出此时点P的坐标;若不存在,请说明理由.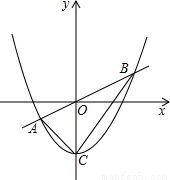
 x与抛物线y=ax2+b(a≠0)交于A(-4,-2),B(6,3)两点.抛物线与y轴的交点为C.
x与抛物线y=ax2+b(a≠0)交于A(-4,-2),B(6,3)两点.抛物线与y轴的交点为C. ?若存在,试求出此时点P的坐标;若不存在,请说明理由.
?若存在,试求出此时点P的坐标;若不存在,请说明理由.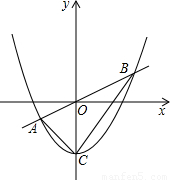
 x与抛物线y=ax2+b(a≠0)交于A(-4,-2),B(6,3)两点.抛物线与y轴的交点为C.
x与抛物线y=ax2+b(a≠0)交于A(-4,-2),B(6,3)两点.抛物线与y轴的交点为C. ?若存在,试求出此时点P的坐标;若不存在,请说明理由.
?若存在,试求出此时点P的坐标;若不存在,请说明理由.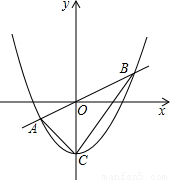
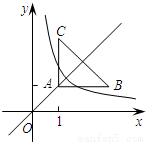
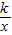 (k≠0)与△ABC有交点,则k的取值范围是( )
(k≠0)与△ABC有交点,则k的取值范围是( )