题目内容
(2009•义乌)如图,AB是⊙O的直径,BC⊥AB于点B,连接OC交⊙O于点E,弦AD∥OC,弦DF⊥AB于点G.(1)求证:点E是
 的中点;
的中点;(2)求证:CD是⊙O的切线;
(3)若sin∠BAD=
 ,⊙O的半径为5,求DF的长.
,⊙O的半径为5,求DF的长.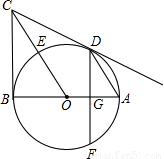
【答案】分析:(1)根据AD∥OC可得∠A=∠COB,从而判定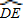 =
=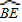 ;
;
(2)连接OD,只要证明∠CDO=90°即可;
(3)在△ADG中用勾股定理求解.
解答: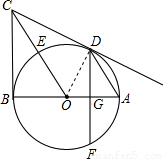 (1)证明:连接OD;
(1)证明:连接OD;
∵AD∥OC,
∴∠A=∠COB;(1分)
∵∠A= ∠BOD,
∠BOD,
∴∠BOC= ∠BOD;
∠BOD;
∴∠DOC=∠BOC;
∴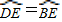 ,
,
则点E是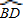 的中点;(2分)
的中点;(2分)
(2)证明:如图所示:
由(1)知∠DOE=∠BOE,(1分)
∵CO=CO,OD=OB,
∴△COD≌△COB;(2分)
∴∠CDO=∠B;
又∵BC⊥AB,
∴∠CDO=∠B=90°;
∴CD是⊙O的切线;(3分)
(3)解:在△ADG中,∵sinA=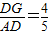 ,
,
设DG=4x,AD=5x;
∵DF⊥AB,
∴AG=3x;(1分)
又∵⊙O的半径为5,
∴OG=5-3x;
∵OD2=DG2+OG2,
∴52=(4x)2+(5-3x)2;(2分)
∴x1= ,x2=0;(舍去)
,x2=0;(舍去)
∴DF=2DG=2×4x=8x=8×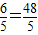 (3分).
(3分).
点评:本题考查了圆周角的性质,切线的判定和勾股定理的运用.
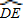 =
=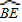 ;
;(2)连接OD,只要证明∠CDO=90°即可;
(3)在△ADG中用勾股定理求解.
解答:
 (1)证明:连接OD;
(1)证明:连接OD;∵AD∥OC,
∴∠A=∠COB;(1分)
∵∠A=
 ∠BOD,
∠BOD,∴∠BOC=
 ∠BOD;
∠BOD;∴∠DOC=∠BOC;
∴
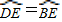 ,
,则点E是
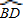 的中点;(2分)
的中点;(2分)(2)证明:如图所示:
由(1)知∠DOE=∠BOE,(1分)
∵CO=CO,OD=OB,
∴△COD≌△COB;(2分)
∴∠CDO=∠B;
又∵BC⊥AB,
∴∠CDO=∠B=90°;
∴CD是⊙O的切线;(3分)
(3)解:在△ADG中,∵sinA=
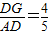 ,
,设DG=4x,AD=5x;
∵DF⊥AB,
∴AG=3x;(1分)
又∵⊙O的半径为5,
∴OG=5-3x;
∵OD2=DG2+OG2,
∴52=(4x)2+(5-3x)2;(2分)
∴x1=
 ,x2=0;(舍去)
,x2=0;(舍去)∴DF=2DG=2×4x=8x=8×
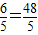 (3分).
(3分).点评:本题考查了圆周角的性质,切线的判定和勾股定理的运用.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目




