Question

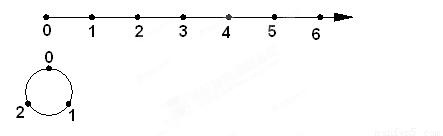
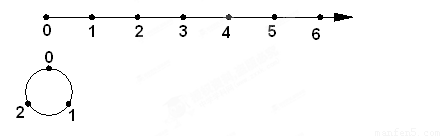
如图所示，按下列方法将数轴的正半轴绕在一个圆上（该圆周长为3个单位长，且在圆周的三等分点处分别标上了数字0，1，2）上：先让原点与圆周上0所对应的点重合，再将正半轴按顺时针方向绕在该圆周上，使数轴上1，2，3，4，…所对应的点分别与圆周上1，2，0，1，…所对应的点重合，这样，正半轴上的整数就与圆周上的数字建立了一种对应关系．

（1）圆周上数字a与数轴上的数5对应，则a=

2

；
（2）数轴上的一个整数点刚刚绕过圆周n圈（n为正整数）后，并落在圆周上数字1所对应的位置，这个整数是

3n+1

 （用含n的代数式表示）．

Answer 1

分析：先找出正半轴上的整数与圆周上的数字建立的对应关系，找出规律进行解答即可．

解答：解：（1）∵数轴上1，2，3，4，…所对应的点分别与圆周上1，2，0，1，…所对应的点重合，
∴圆周上数字a与数轴上的数5对应时a=2；

（2）∵数轴上1，2，3，4，…所对应的点分别与圆周上1，2，0，1，…所对应的点重合，
∴圆周上了数字0、1、2与正半轴上的整数每3个一组0、1、2，3、4、5，6、7、8，…分别对应，
∴数轴上的一个整数点刚刚绕过圆周n圈（n为正整数）后，并落在圆周上数字1所对应的位置，这个整数是3n+1．
故答案为：a=2；3n+1．

点评：本题考查的是数轴的特点，先根据题意找出规律是解答此题的关键．