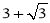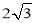Question

如图1，正方形ABCD与正方形AEFG的边AB、AE（AB＜AE）在一条直线上，正方形AEFG以点A为旋转中心逆时针旋转，设旋转角为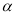. 在旋转过程中，两个正方形只有点A重合，其它顶点均不重合，连接BE、DG.

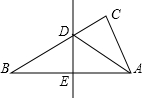
（1）当正方形AEFG旋转至如图2所示的位置时，求证：BE=DG；

（2）当点C在直线BE上时，连接FC，直接写出∠FCD 的度数；

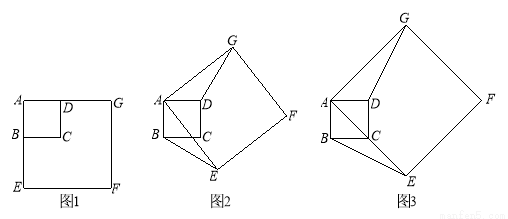
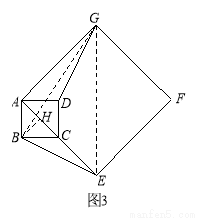
（3）如图3，如果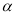=45°，AB =2，AE=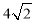，求点G到BE的距离.

 

 

Answer 1

（1）证明见解析；（2）45°或135°；（3）.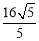

【解析】

试题分析：（1）根据正方形的性质可得AB=AD，AE=AG，∠BAD=∠EAG=90°，再求出∠BAE=∠DAG，然后利用“边角边”证明△ABE和△ADG全等，根据全等三角形对应边相等证明即可.

（2）当点C在直线BE上时，可知点E与C重合或G点C与重合，据此求解即可.

（3）根据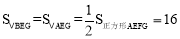和求解即可.

试题解析：（1）如图2，∵四边形ABCD是正方形，∴AB=AD，∠BAE+∠EAD=90°.

∵四边形AEFG是正方形，∴AE=AG，∠EAD+∠DAG=90°.

∴∠BAE=∠DAG..

∴△ABE≌△ADG（SAS）.

∴BE=DG..

（2）如图，当点C在直线BE上时，可知点E与C重合或G点C与重合，此时∠FCD 的度数为45°或135°.

（3）如图3，连接GB、GE.

由已知α=45°，可知∠BAE=45°.

又∵GE为正方形AEFG的对角线， ∴∠AEG=45°.∴AB∥GE.

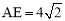∵，∴GE =8.

∴.

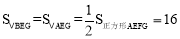过点B作BH⊥AE于点H.

∵AB=2，∴. ∴. .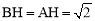

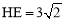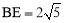设点G到BE的距离为h.

∴.

∴.

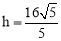∴点G到BE的距离为.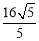

考点：1.旋转的性质；2.正方形的性质；3.全等三角形的判定和性质；4.平行的判定和性质；5.勾股定理；6.分类思想的应用．