题目内容
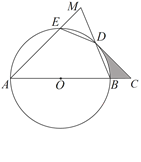
【题目】如图,AB是⊙O的直径,弧ED=弧BD,连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.
(1)若OA![]() CD
CD![]()
![]() ,求阴影部分的面积;
,求阴影部分的面积;
(2)求证:DE![]() DM.
DM.
【答案】(1)4-π;(2)参见解析.
【解析】
试题(1)连接OD,由已知条件可证出三角形ODC是等腰直角三角形,OD的长度知道,∠DOB的度数是45度,这样,阴影的面积就等于等腰直角三角形ODC的面积减去扇形ODB的面积.(2)连接AD,由已知条件可证出AD垂直平分BM,从而得到DM=DB,又因为弧DE=弧DB,DE=DB,所以DE就等于DM了.
试题解析:(1)连接OD,∵CD是⊙O切线,∴OD⊥CD∵OA="CD" =![]() , OA=OD∴OD=CD=
, OA=OD∴OD=CD=![]() ∴△OCD 为等腰直角三角形∠DOC=∠C=45°S阴影=S△OCD-S扇OBD=
∴△OCD 为等腰直角三角形∠DOC=∠C=45°S阴影=S△OCD-S扇OBD=![]() ×
×![]() ×
×![]() -
-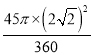
![]() .(2)连接AD.∵AB是⊙O直径∴∠ADB=∠ADM= 90°又∵弧ED=弧BD∴ED="BD" ∠MAD=∠BAD∴△AMD≌△ABD∴DM="BD" ∴DE=DM.如图所示:
.(2)连接AD.∵AB是⊙O直径∴∠ADB=∠ADM= 90°又∵弧ED=弧BD∴ED="BD" ∠MAD=∠BAD∴△AMD≌△ABD∴DM="BD" ∴DE=DM.如图所示:


练习册系列答案
相关题目