题目内容
已知整数x,y,z满足x≤y<z,且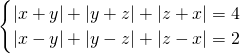 ,那么x2+y2+z2的值等于
,那么x2+y2+z2的值等于
- A.2
- B.14
- C.2或14
- D.14或17
A
分析:根据绝对值的定义和已知条件,得出|x+y|,|x-y|式子的范围,把已知访化简,从而确定x,y,z的范围即可求解.
解答:∵x≤y<z,
∴|x-y|=y-x,|y-z|=z-y,|z-x|=z-x,
因而第二个方程可以化简为:
2z-2x=2,即z=x+1,
∵x,y,z是整数,
根据条件 ,
,
则 两式相加得到:-3≤x≤3,
两式相加得到:-3≤x≤3,
两式相减得到:-1≤y≤1,
同理: ,得到-1≤z≤1,
,得到-1≤z≤1,
根据x,y,z是整数讨论可得:x=y=-1,z=0或x=1,y=z=0此时第一个方程不成立,故舍去.
∴x2+y2+z2=(-1)2+(-1)2+0=2.
故本题答案为:2.
点评:本题考查了绝对值的定义和三元一次方程组的解法,确定x,y,z的范围是解题的关键.
分析:根据绝对值的定义和已知条件,得出|x+y|,|x-y|式子的范围,把已知访化简,从而确定x,y,z的范围即可求解.
解答:∵x≤y<z,
∴|x-y|=y-x,|y-z|=z-y,|z-x|=z-x,
因而第二个方程可以化简为:
2z-2x=2,即z=x+1,
∵x,y,z是整数,
根据条件
 ,
,则
 两式相加得到:-3≤x≤3,
两式相加得到:-3≤x≤3,两式相减得到:-1≤y≤1,
同理:
 ,得到-1≤z≤1,
,得到-1≤z≤1,根据x,y,z是整数讨论可得:x=y=-1,z=0或x=1,y=z=0此时第一个方程不成立,故舍去.
∴x2+y2+z2=(-1)2+(-1)2+0=2.
故本题答案为:2.
点评:本题考查了绝对值的定义和三元一次方程组的解法,确定x,y,z的范围是解题的关键.

练习册系列答案
相关题目
我市部分学生参加了2004年全国初中数学竞赛决赛,并取得优异成绩.已知竞赛成绩分数都是整数,试题满分为140分,参赛学生的成绩分数分布情况如下:
请根据以上信息解答下列问题:
(1)全市共有多少人参加本次数学竞赛决赛最低分和最高分在什么分数范围?
(2)经竞赛组委会评定,竞赛成绩在60分以上(含60分)的考生均可获得不同等级的奖励,求我市参加本次竞赛决赛考生的获奖比例;
(3)决赛成绩分数的中位数落在哪个分数段内?
(4)上表还提供了其他信息,例如:“没获奖的人数为105人”等等.请你再写出两条此表提供的信息.
| 分数段 | 0-19 | 20-39 | 40-59 | 60-79 | 80-99 | 100-119 | 120-140 |
| 人 数 | 0 | 37 | 68 | 95 | 56 | 32 | 12 |
(1)全市共有多少人参加本次数学竞赛决赛最低分和最高分在什么分数范围?
(2)经竞赛组委会评定,竞赛成绩在60分以上(含60分)的考生均可获得不同等级的奖励,求我市参加本次竞赛决赛考生的获奖比例;
(3)决赛成绩分数的中位数落在哪个分数段内?
(4)上表还提供了其他信息,例如:“没获奖的人数为105人”等等.请你再写出两条此表提供的信息.
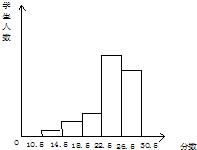 3、某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频率分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46.
3、某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频率分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46.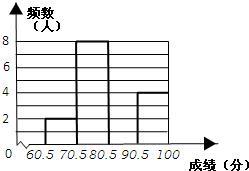
 12、阳光中学举行应用数学知识竞赛.已知竞赛成绩都是整数,试题满分为140分,现从参赛学生中随机抽取100名学生的成绩进行统计分析,得到如下图:
12、阳光中学举行应用数学知识竞赛.已知竞赛成绩都是整数,试题满分为140分,现从参赛学生中随机抽取100名学生的成绩进行统计分析,得到如下图: