题目内容
等腰梯形中位线长是b,对角线平分腰和上底的夹角,下底比周长小a,则上底的长是________.
4b-a
分析:首先根据题意作出图形,有梯形的中位线性质,可得:AD+BC=2b,又由对角线平分腰和上底的夹角,可证得BC=CD,设BC=x,利用方程思想求解即可得到答案.
解答: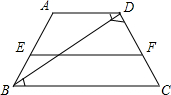 解:
解:
∵等腰梯形中位线长是b,
∴AD+BC=2b,AD∥BC,AB=CD,
∴∠1=∠3,
∵对角线平分腰和上底的夹角,
∴∠1=∠2,
∴∠2=∠3,
∴BC=CD,
设BC=x,则AB=CD=BC=x,AD=2b-x,
∵下底比周长小a,
∴x+a=3x+2b-x,
解得:x=a-2b,
∴AD=2b-(a-2b)=4b-a.
故上底的长是4b-a.
故答案为:4b-a.
点评:此题考查了梯形的中位线的性质和等腰三角形的判定.解此题的关键是要注意数形结合与方程思想的应用.
分析:首先根据题意作出图形,有梯形的中位线性质,可得:AD+BC=2b,又由对角线平分腰和上底的夹角,可证得BC=CD,设BC=x,利用方程思想求解即可得到答案.
解答:
 解:
解:∵等腰梯形中位线长是b,
∴AD+BC=2b,AD∥BC,AB=CD,
∴∠1=∠3,
∵对角线平分腰和上底的夹角,
∴∠1=∠2,
∴∠2=∠3,
∴BC=CD,
设BC=x,则AB=CD=BC=x,AD=2b-x,
∵下底比周长小a,
∴x+a=3x+2b-x,
解得:x=a-2b,
∴AD=2b-(a-2b)=4b-a.
故上底的长是4b-a.
故答案为:4b-a.
点评:此题考查了梯形的中位线的性质和等腰三角形的判定.解此题的关键是要注意数形结合与方程思想的应用.

练习册系列答案
相关题目