题目内容
如果有理数a满足|a|+a=0，a≠-1，则
的值等于（ ）
| |a|-1 |
| |a+1| |
| A、1 | B、-1 |
| C、0或1 | D、1或-1 |
分析：根据|a|+a=0可得|a|=-a，从而可确定a≤0，为了去掉|a+1|的绝对，需要分类讨论，①-1≤a≤0，②a＜-1，这样去掉绝对值后进行分式的运算即可．
解答：解：∵|a|+a=0，
∴|a|=-a，a≤0，
①当-1＜a≤0时，
=
=-1；
②当a＜-1时，
=
=1，
综上可得
=1或-1．
故选D．
∴|a|=-a，a≤0，
①当-1＜a≤0时，
| |a|-1 |
| |a+1| |
| -a-1 |
| a+1 |
②当a＜-1时，
| |a|-1 |
| |a+1| |
| -a-1 |
| -a-1 |
综上可得
| |a|-1 |
| |a+1| |
故选D．
点评：本题考查了有理数无理数的概念及计算，解答本题的关键是判断出a≤0后分类讨论a的范围，去掉|a+1|的绝对值，难度一般．
练习册系列答案
相关题目
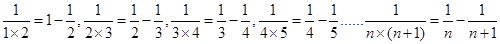请完成下面的问题:
+…+
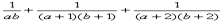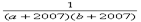的值
+…+
的值。