题目内容
如果圆中一条弦长与半径相等,那么此弦所对的圆周角的度数为 .
【答案】分析:弦长与半径相等,连接圆心和弦的端点,可得等边三角形,那么圆心角为60°,那么这条弦所对的优弧上的圆周角为30°,则劣弧上的圆周角为150°.
解答: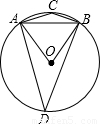 解:如图
解:如图
若AB=OA=OB,则
∠AOB=60°
∴∠D= ∠AOB=30°
∠AOB=30°
∠C=180°-∠D=150°.
点评:解决本题的关键是得到这条弦所对的圆心角的度数.本题需注意:在一个圆中,弦所对的圆周角是两个,它们互为补角.
解答:
 解:如图
解:如图若AB=OA=OB,则
∠AOB=60°
∴∠D=
 ∠AOB=30°
∠AOB=30°∠C=180°-∠D=150°.
点评:解决本题的关键是得到这条弦所对的圆心角的度数.本题需注意:在一个圆中,弦所对的圆周角是两个,它们互为补角.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目