题目内容
(11·孝感)(满分10分)已知关于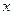 的方程
的方程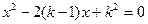 有两个实数根
有两个实数根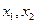 .
.(1)求
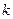 的取值范围;(4分)
的取值范围;(4分)(2)若
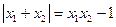 ,求
,求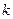 的值;(6分)
的值;(6分)
解:(1)依题意得△≥0,即[-2(k-1)]2-4k2≥0……………………………2分
 (2)依题意x1+x2=2(k-1),x1·x2=k2 …………………………………………………5分
(2)依题意x1+x2=2(k-1),x1·x2=k2 …………………………………………………5分
以下分两种情况讨论:
①当x1+x2≥0时,则有x1+x2=x1·x2-1,即2(k-1)=k2-1
解得k1=k2=1

∴k1=k2=1不合题意,舍去……………………………………………7分
②当x1+x2<0时,则有x1+x2=-(x1·x2-1),即2(k-1)=-(k2-1)
解得k1=1,k2=-3
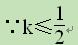
∴k=-3……………………………………………9分
综合①、②可知k=-3……………………………………………10分
说明:第(2)问另外解法:依题意可知x1+x2=2(k-1)

∴2(k-1)<0即x1+x2<0……………………………………………7分
∴-2(k-1)=k2-1
解得k1=1,k2=-3…………………………………9分
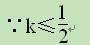
∴k=-3……………………………………………10分解析:
略
 (2)依题意x1+x2=2(k-1),x1·x2=k2 …………………………………………………5分
(2)依题意x1+x2=2(k-1),x1·x2=k2 …………………………………………………5分以下分两种情况讨论:
①当x1+x2≥0时,则有x1+x2=x1·x2-1,即2(k-1)=k2-1
解得k1=k2=1

∴k1=k2=1不合题意,舍去……………………………………………7分
②当x1+x2<0时,则有x1+x2=-(x1·x2-1),即2(k-1)=-(k2-1)
解得k1=1,k2=-3
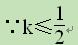
∴k=-3……………………………………………9分
综合①、②可知k=-3……………………………………………10分
说明:第(2)问另外解法:依题意可知x1+x2=2(k-1)

∴2(k-1)<0即x1+x2<0……………………………………………7分
∴-2(k-1)=k2-1
解得k1=1,k2=-3…………………………………9分
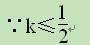
∴k=-3……………………………………………10分解析:
略

练习册系列答案
相关题目
 的方程
的方程 有两个实数根
有两个实数根 .
. 名学生的升学意向,并根据调查结果绘制出如下两幅不完整的统计图.请你根据图中的信息解答下列问题:
名学生的升学意向,并根据调查结果绘制出如下两幅不完整的统计图.请你根据图中的信息解答下列问题: