题目内容
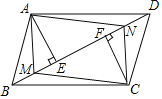
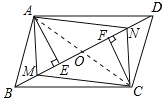
【题目】如图,BD是ABCD的对角线,AE⊥BD,CF⊥BD,垂足分别为E,F,AM与CN分别是∠BAE与∠DCF的平分线,AM交BE于点M,CN交DF于点N,连接AN,CM.求证:四边形AMCN是平行四边形.
【答案】见解析.
【解析】
连接AC交BD于O,由平行四边形的性质得出OA=OC,OB=OD,AB=CD,AB∥CD,由ASA证明△ABM≌△CDN,得出BM=DN,证出OM=ON,即可得出结论.
证明:连接AC交BD于O,如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AB=CD,AB∥CD,
∴∠ABM=∠CDN,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
∴∠ABM+∠BAE=90°,∠CDN+∠DCF=90°,
∴∠BAE=∠DCF,
∵AM与CN分别是∠BAE与∠DCF的平分线,
∴∠BAM=∠DCN,
在△ABM和△CDN中,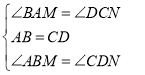 ,
,
∴△ABM≌△CDN(ASA),
∴BM=DN,
∴OM=ON,
又∵OA=OC,
∴四边形AMCN是平行四边形.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目