题目内容
已知一直角三角形的周长是 ,斜边上的中线长2,则这个三角形的面积是( )
,斜边上的中线长2,则这个三角形的面积是( )
A.5 B. C.
C. D.1
D.1
【答案】
B
【解析】
试题分析:根据直角三角形的性质:在直角三角形中,斜边上的中线等于斜边的一半,可求得斜边的长,再根据直角三角形的周长和勾股定理,可求得两直角边的长或长的乘积,由此可求出这个三角形的面积.
设两直角边分别为a,b,斜边为c,
根据三角形的性质知:c=4,
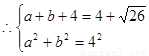 ,
,
解得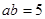 ,
,
则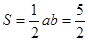 ,
,
故选B.
考点:本题考查的是直角三角形的性质
点评:解答本题的关键是熟练掌握直角三角形的性质:在直角三角形中,斜边上的中线等于斜边的一半。在解题过程中,应了解直角三角形的一些特殊性质,在进行求解的时候使问题变得简单.

练习册系列答案
相关题目
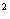 ,r为底面半径).因一个直角三角形有两条直角边,故本题有两种方案:
,r为底面半径).因一个直角三角形有两条直角边,故本题有两种方案: