题目内容
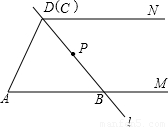
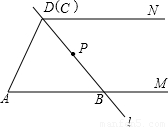
（2003•三明）已知：如图，线段AM∥DN，直线l与AM、DN分别交于点B、C，直线l绕BC的中点P旋转（点C由D点向N点方向移动）．（1）线段BC与AD、AB、CD围成的图形，在初始状态下，形状是△ABD（即△ABC），请你写出变化过程中其余的各种特殊四边形名称；
（2）任取变化过程中的两个图形，测量AB、CD长度后分别计算同一个图形的AB+CD（精确到1cm），比较这两个和是否相同，试加以证明．
【答案】分析：（1）因为AM∥DN，所以移动出去就可以得到梯形，移动过程中，DC变长AB变短，可以有等腰梯形、直角梯形、平行四边形．
（2）点P是中点，取AD的中点P′，不论怎么移动，PP′都是所得图形的中位线AB+CD=2PP′，所以相等．
解答：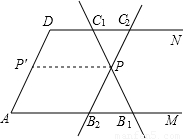
解：（1）等腰梯形、直角梯形、平行四边形．
（2）∵经测量、计算，两个图形的AB+CD都等于4cm．（精确到1cm）
∴这两个和相同．（对原试卷的图形而言）
证明：过点P作PP'∥AM交AD于点P'
∴PP'是梯形AB1C1D的中位线
∴AB1+C1D=2PP'，同理AB2+C2D=2PP'
∴这两个和是相同的．（注：还可用三角形全等证明）
点评：本题考查特殊四边形的定义和把变化的线段的长通过中位线转化成不变的量进行求解，这也是本题的难点．
（2）点P是中点，取AD的中点P′，不论怎么移动，PP′都是所得图形的中位线AB+CD=2PP′，所以相等．
解答：
解：（1）等腰梯形、直角梯形、平行四边形．（2）∵经测量、计算，两个图形的AB+CD都等于4cm．（精确到1cm）
∴这两个和相同．（对原试卷的图形而言）
证明：过点P作PP'∥AM交AD于点P'
∴PP'是梯形AB1C1D的中位线
∴AB1+C1D=2PP'，同理AB2+C2D=2PP'
∴这两个和是相同的．（注：还可用三角形全等证明）
点评：本题考查特殊四边形的定义和把变化的线段的长通过中位线转化成不变的量进行求解，这也是本题的难点．
练习册系列答案
相关题目
