题目内容
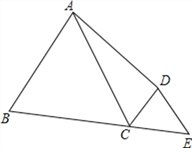
【题目】如图,已知AB=AD,∠BAD=60°,∠BCD=120°,延长BC,使CE=CD,连接DE,求证:BC+DC=AC.
思路点拨:
(1)由已知条件AB=AD,∠BAD=60°,可知:△ABD是 三角形;
(2)同理由已知条件∠BCD=120°得到∠DCE= ,且CE=CD,可知 ;
(3)要证BC+DC=AC,可将问题转化为两条线段相等,即 = ;请你先完成思路点拨,再进行证明:
【答案】(1)等边.(2)60°,△DCE是等边三角形.(3)BE=AC,证明见解析。
【解析】分析:(1)连接BD,根据等边三角形判定推出即可;(2)求出∠DCE=60°,得到等边三角形DCE即可;(3)根据等边三角形性质推出AD=BD,CD=DE,∠ADB=∠CDE=60°,推出∠ADC=∠BDE,证△ADC≌△BDE即可;
本题解析:(1)等边.(2)60°,△DCE是等边三角形.
(3)BE=AC.
证明:连接BD,
∵AB=AD,∠BAD=60°,∴△ABD是等边三角形,
∵∠BCD=120°,
∴∠DCE=180°-∠BCD=180°-120°=60°,
∵CE=CD,
∴△DCE是等边三角形,
∵等边三角形ABD和DCE,
∴AD=BD,CD=DE,∠ADB=∠CDE=60°,
∴∠ADB+∠BDC=∠CDE+∠BDC,
即∠ADC=∠BDE,
在△ADC和△BDE中,AD=BD,∠ADC=∠BDE, DC=DE,
∴△ADC≌△BDE,
∴AC=BE=BC+CE =BC+DC,
∴BC+DC=AC


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目