题目内容
张辉在做实验室做“盐水”实验.当他用玻璃棒搅动烧杯底部的食盐时发现手中的玻璃棒离开烧杯口长度在不断的变化.若烧杯底的半径为2.5cm,高为12cm,玻璃棒的长度为20cm,请你帮助张辉算出玻璃棒露出烧杯口部分x的范围是________.
7cm≤x≤8cm
分析:由于玻璃棒、烧杯内部底面直径与杯壁正好构成直角三角形,故可先利用勾股定理求出AB的长,进而可得出结论.
解答: 解:如图所示:
解:如图所示:
∵杯子底面半径为2.5cm,高为12cm,
∴BC=2×2.5=5cm,AC=12cm,
∵玻璃棒、烧杯内部底面直径与杯壁正好构成直角三角形,
∴AB=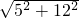 =13cm,
=13cm,
∴此时露出烧杯外部分为20-13=7cm,
当玻璃棒与杯底垂直时露在外面最多为:20-12=8cm,
∴玻璃棒露出烧杯口部分x的范围是7cm≤x≤8cm
故答案为:7cm≤x≤8cm
点评:本题考查的是勾股定理在实际生活中的运用,解答此类题目的关键是构造出直角三角形,再利用勾股定理解答.
分析:由于玻璃棒、烧杯内部底面直径与杯壁正好构成直角三角形,故可先利用勾股定理求出AB的长,进而可得出结论.
解答:
 解:如图所示:
解:如图所示:∵杯子底面半径为2.5cm,高为12cm,
∴BC=2×2.5=5cm,AC=12cm,
∵玻璃棒、烧杯内部底面直径与杯壁正好构成直角三角形,
∴AB=
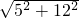 =13cm,
=13cm,∴此时露出烧杯外部分为20-13=7cm,
当玻璃棒与杯底垂直时露在外面最多为:20-12=8cm,
∴玻璃棒露出烧杯口部分x的范围是7cm≤x≤8cm
故答案为:7cm≤x≤8cm
点评:本题考查的是勾股定理在实际生活中的运用,解答此类题目的关键是构造出直角三角形,再利用勾股定理解答.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目