题目内容
下列语句中正确的有( )个
(1)有两个角相等的梯形一定是等腰梯形
(2)一组对边平行,另一组对边相等的四边形是平行四边形
(3)一组对边平行,一组对角相等的四边形是平行四边形
(4)一个多边形的每一个内角都是150°,则这是一个十二边形.
(1)有两个角相等的梯形一定是等腰梯形
(2)一组对边平行,另一组对边相等的四边形是平行四边形
(3)一组对边平行,一组对角相等的四边形是平行四边形
(4)一个多边形的每一个内角都是150°,则这是一个十二边形.
分析:根据直角梯形定义即可判断(1);
根据等腰梯形和平行四边形的判定即可判断(2);
根据平行线的性质和已知推出∠A=∠C,根据平行四边形的判定得出平行四边形ABCD,即可判断(3);
设这个多边形的边数是n,则
=150°,求出方程的解即可.
根据等腰梯形和平行四边形的判定即可判断(2);
根据平行线的性质和已知推出∠A=∠C,根据平行四边形的判定得出平行四边形ABCD,即可判断(3);
设这个多边形的边数是n,则
| (n-2)•180° |
| n |
解答: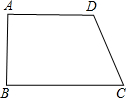 解:如直角梯形ABCD,AD∥BC,∠A=∠B=90°,但不是等腰梯形,∴(1)错误;
解:如直角梯形ABCD,AD∥BC,∠A=∠B=90°,但不是等腰梯形,∴(1)错误;
一组对边平行,另一组对边相等的四边形可能是等腰梯形,不一定是平行四边形,∴(2)错误;
∵AD∥BC,
∴∠A+∠B=180°,∠D+∠C=180°,
∵∠B=∠D,
∴∠A=∠C,
∴四边形ABCD是平行四边形,∴(3)正确;
设这个多边形的边数是n,则
=150°,
∴n=12,∴(4)正确;
即正确的命题有2个,
故选B.
 解:如直角梯形ABCD,AD∥BC,∠A=∠B=90°,但不是等腰梯形,∴(1)错误;
解:如直角梯形ABCD,AD∥BC,∠A=∠B=90°,但不是等腰梯形,∴(1)错误;一组对边平行,另一组对边相等的四边形可能是等腰梯形,不一定是平行四边形,∴(2)错误;
∵AD∥BC,
∴∠A+∠B=180°,∠D+∠C=180°,
∵∠B=∠D,

∴∠A=∠C,
∴四边形ABCD是平行四边形,∴(3)正确;
设这个多边形的边数是n,则
| (n-2)•180° |
| n |
∴n=12,∴(4)正确;
即正确的命题有2个,
故选B.
点评:本题考查了平行四边形的判定,等腰梯形的判定,直角梯形,多边形的内角和定理等知识点的运用,能综合运用性质进行推理是解此题的关键,题目比较好,但是一道比较容易出错的题目.

练习册系列答案
相关题目