��Ŀ����
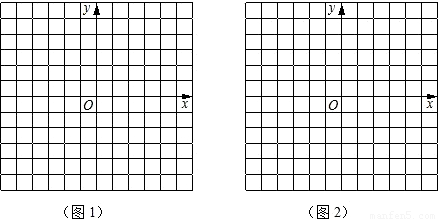
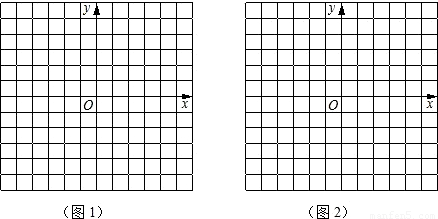
��2006•���ݣ���1������ͼ1��ʾ��ƽ��ֱ������ϵ�л�����A��2��3�����ٻ�����A����y��ĶԳƵ�A'�����A'������Ϊ______����2����ͼ1�л�������A��ԭ��O��ֱ��l����ֱ��l�ĺ�����ϵʽΪ______���ٻ���ֱ��l����y��ԳƵ�ֱ��l'����ֱ��l'�ĺ�����ϵʽΪ______��
��3����ͼ2�л���ֱ��y=2x+4����ֱ��m�����ٻ���ֱ��m����y��ԳƵ�ֱ��m'����ֱ��m'�ĺ�����ϵʽΪ______��
��4����������Լ��ڽ����������Ĺ���������õľ���ش�ֱ��y=kx+b��k��bΪ������k��0������y��ԳƵ�ֱ�ߵĺ�����ϵʽΪ______��
���𰸡���������1������y��Գƣ������껥Ϊ�෴���������겻�䣮
��2��Ϊ��������������Ϊy=kx����2��3���ʺϣ������k= ��ͬ���ɵù���y��ԳƵĺ�������ʽ��
��ͬ���ɵù���y��ԳƵĺ�������ʽ��
��3������ԭ����ʽ�������㣨0��4������1��6�����������㻭ֱ���ɣ��ȵõ�ǰ��������Ĺ���y��ԳƵĵ㣨0��4������-1��6����ֱ���ɣ��ô���ϵ����������ú�������ʽ��
��4���۲�ɵ�������������y��Գƣ���k��Ϊ�෴����b���䣮
����⣺��1��A�䣨-2��3������1�֣�
��2��y= x�������л�ͼ1�֣���3�֣�
x�������л�ͼ1�֣���3�֣�
y=- x���������л�ͼ1�֣���5�֣�
x���������л�ͼ1�֣���5�֣�
��3��y=-2x+4�����л�ͼ1�֣���7�֣�
��4��y=-kx+b����8�֣�
�����������ʽͨ���ô���ϵ�����������y��Գƣ��������겻�䣬�����껥Ϊ�෴����������������y��Գƣ���k��Ϊ�෴����b���䣮
��2��Ϊ��������������Ϊy=kx����2��3���ʺϣ������k=
 ��ͬ���ɵù���y��ԳƵĺ�������ʽ��
��ͬ���ɵù���y��ԳƵĺ�������ʽ����3������ԭ����ʽ�������㣨0��4������1��6�����������㻭ֱ���ɣ��ȵõ�ǰ��������Ĺ���y��ԳƵĵ㣨0��4������-1��6����ֱ���ɣ��ô���ϵ����������ú�������ʽ��
��4���۲�ɵ�������������y��Գƣ���k��Ϊ�෴����b���䣮
����⣺��1��A�䣨-2��3������1�֣�
��2��y=
 x�������л�ͼ1�֣���3�֣�
x�������л�ͼ1�֣���3�֣�y=-
 x���������л�ͼ1�֣���5�֣�
x���������л�ͼ1�֣���5�֣���3��y=-2x+4�����л�ͼ1�֣���7�֣�
��4��y=-kx+b����8�֣�
�����������ʽͨ���ô���ϵ�����������y��Գƣ��������겻�䣬�����껥Ϊ�෴����������������y��Գƣ���k��Ϊ�෴����b���䣮

��ϰ��ϵ�д�
 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�
�����Ŀ
��2006•���ݣ��±������˴���ʽx2+bx+c��x��һЩ��Ӧֵ��
��1�����ڱ��ڵĿո��������ʵ�������
��2����y=x2+bx+c����xȡ��ֵʱ��y��0��
��3����˵����������ƽ�ƺ���y=x2+bx+c��ͼ��õ�����y=x2��ͼ��
| x | �� | 0 | 1 | 2 | 3 | 4 | �� |
| x2+bx+c | �� | 3 | -1 | 3 | �� |
��2����y=x2+bx+c����xȡ��ֵʱ��y��0��
��3����˵����������ƽ�ƺ���y=x2+bx+c��ͼ��õ�����y=x2��ͼ��
��2006•���ݣ��±������˴���ʽx2+bx+c��x��һЩ��Ӧֵ��
��1�����ڱ��ڵĿո��������ʵ�������
��2����y=x2+bx+c����xȡ��ֵʱ��y��0��
��3����˵����������ƽ�ƺ���y=x2+bx+c��ͼ��õ�����y=x2��ͼ��
| x | �� | 0 | 1 | 2 | 3 | 4 | �� |
| x2+bx+c | �� | 3 | -1 | 3 | �� |
��2����y=x2+bx+c����xȡ��ֵʱ��y��0��
��3����˵����������ƽ�ƺ���y=x2+bx+c��ͼ��õ�����y=x2��ͼ��
��2006•���ݣ��±������˴���ʽx2+bx+c��x��һЩ��Ӧֵ��
��1�����ڱ��ڵĿո��������ʵ�������
��2����y=x2+bx+c����xȡ��ֵʱ��y��0��
��3����˵����������ƽ�ƺ���y=x2+bx+c��ͼ��õ�����y=x2��ͼ��
| x | �� | 0 | 1 | 2 | 3 | 4 | �� |
| x2+bx+c | �� | 3 | -1 | 3 | �� |
��2����y=x2+bx+c����xȡ��ֵʱ��y��0��
��3����˵����������ƽ�ƺ���y=x2+bx+c��ͼ��õ�����y=x2��ͼ��