题目内容
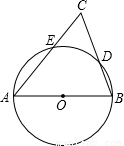
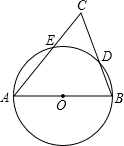如图所示，以锐角△ABC的边AB为直径作⊙O，交AC，BC于E、D两点，若AC=14，CD=4，7sinC=3tanB，则BD=分析：连接AD，分别在Rt△ACD和Rt△ABD中，表示出sinC和tanB的值，根据它们的比例关系，即可求得BD、AC的关系式，进而代值计算即可．
解答：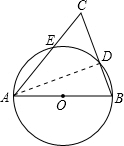
解：连接AD，则AD⊥BC．
在Rt△ADC中，sinC=
；
在Rt△ABD中，tanB=
．
∵7sinC=3tanB，
∴
=
．
即：
×
=
，
∴
=
．
∵AC=14，
∴BD=6．
解：连接AD，则AD⊥BC．在Rt△ADC中，sinC=
| AD |
| AC |
在Rt△ABD中，tanB=
| AD |
| BD |
∵7sinC=3tanB，
∴
| sinC |
| tanB |
| 3 |
| 7 |
即：
| AD |
| AC |
| BD |
| AD |
| 3 |
| 7 |
∴
| BD |
| AC |
| 3 |
| 7 |
∵AC=14，
∴BD=6．
点评：此题主要考查的是圆周角定理和锐角三角函数的定义，以AD为介质来得到AC、BD的比例关系，是解决问题的关键．
练习册系列答案
相关题目
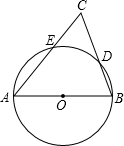如图所示，以锐角△ABC的边AB为直径作⊙O，交AC，BC于E、D两点，若AC=14，CD=4，7sinC=3tanB，则BD=________．
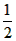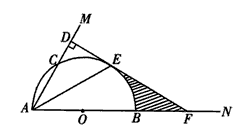
，AE=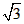
，求阴影部分的面积。
