题目内容
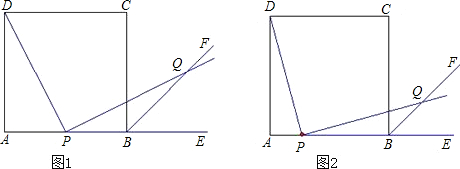
已知点E是边长为2的正方形ABCD的AB边的延长线上一点,P为边AB上的一个动点(不与A、B重合),直线PF⊥PD,∠EBC的平分线与PF交于点Q.(1)如图1,当P为AB的中点时,求PD的长,并比较PD与PQ长的大小;
(2)如图2,在点P运动过程中,PD与PQ长的大小关系会发生变化吗?为什么?
(3)设PB=x,△BPQ和△PAD的面积分别是S1、S2,又y=
| S2 | S1 |
分析:(1)PA=1,AD=2,由勾股定理PD=
,取AD中点M,连PM,则DM=PB=1,AM=AP=1可通过求得∠PBQ=∠DMP,∠PDM=∠QPB证明△PDM≌△QPB继而推出PD=PQ.
(2)在点P运动过程中,设BP=x(0<x<2),则PA=2-x≠0,在AD取点N,使DN=PB=x,则NA=PA=2-x,连PN,则△PAN为等腰直角三角形,求出∠PND=∠QBP再由(1)知∠QPB=∠PDN所以可证明△PDN≌△QPB?PD=PQ
(3)根据(2)表示出S1=
PB×QH、S2=
AP×AD,y=
=
=
,所以Y随PB的变大而减小.
| 5 |
(2)在点P运动过程中,设BP=x(0<x<2),则PA=2-x≠0,在AD取点N,使DN=PB=x,则NA=PA=2-x,连PN,则△PAN为等腰直角三角形,求出∠PND=∠QBP再由(1)知∠QPB=∠PDN所以可证明△PDN≌△QPB?PD=PQ
(3)根据(2)表示出S1=
| 1 |
| 2 |
| 1 |
| 2 |
| S1 |
| S2 |
| 2 |
| X |
| 2 |
| PB |
解答:解:(1)当P为AB的中点时,PA=1,AD=2,
由勾股定理PD=
=
.(1分)
如图,取AD中点M,连PM,则DM=PB=1,AM=AP=1,
∴∠AMP=45°,∴∠PMD=135°.
∵BQ为直角∠EBC的角平分线,∴∠QBE=45°,∴∠PBQ=135°.
∴∠PBQ=∠DMP(2分)
又∵PF⊥PD,∠DPA+∠FPH=90°
在Rt△PAD中∠DPA+∠PDA=90°,∴∠PDM=∠QPB(3分)
∴△PDM≌△QPB,∴PD=PQ(4分)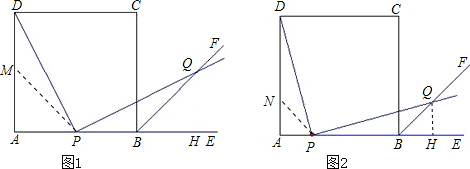
(2)在点P运动过程中,PD=PQ仍然成立.(5分)
证明:在点P运动过程中,设BP=x(0<x<2),则PA=2-x≠0,
同样,在AD取点N,使DN=PB=x,则NA=PA=2-x,连PN,则△PAN为等腰直角三角形,故
∠PNA=45°
∴∠PND=135°,
∴∠PND=∠QBP.(6分)
又由(1)知∠QPB=∠PDN,
∴△PDN≌△QPB,
∴PD=PQ.(7分)
(3)作QH⊥AB于H,则Rt△PDA≌Rt△QPH,即QH=PA=2-x,
∴S1=
PB×QH=
x(2-x)(8分)
又S2=
AP×AD=
×2(2-x)
∴y=
=
=
故知y随PB的增大而减小(或减小而增大).(9分)
由勾股定理PD=
| AD2+AP2 |
| 5 |
如图,取AD中点M,连PM,则DM=PB=1,AM=AP=1,
∴∠AMP=45°,∴∠PMD=135°.
∵BQ为直角∠EBC的角平分线,∴∠QBE=45°,∴∠PBQ=135°.
∴∠PBQ=∠DMP(2分)
又∵PF⊥PD,∠DPA+∠FPH=90°
在Rt△PAD中∠DPA+∠PDA=90°,∴∠PDM=∠QPB(3分)
∴△PDM≌△QPB,∴PD=PQ(4分)

(2)在点P运动过程中,PD=PQ仍然成立.(5分)
证明:在点P运动过程中,设BP=x(0<x<2),则PA=2-x≠0,
同样,在AD取点N,使DN=PB=x,则NA=PA=2-x,连PN,则△PAN为等腰直角三角形,故
∠PNA=45°
∴∠PND=135°,
∴∠PND=∠QBP.(6分)
又由(1)知∠QPB=∠PDN,
∴△PDN≌△QPB,
∴PD=PQ.(7分)
(3)作QH⊥AB于H,则Rt△PDA≌Rt△QPH,即QH=PA=2-x,
∴S1=
| 1 |
| 2 |
| 1 |
| 2 |
又S2=
| 1 |
| 2 |
| 1 |
| 2 |
∴y=
| S2 |
| S1 |
| 2 |
| x |
| 2 |
| PB |
故知y随PB的增大而减小(或减小而增大).(9分)
点评:本题主要考查三角形的全等及正方形的性质,注意在变化中寻找不变,深挖条件.

练习册系列答案
相关题目
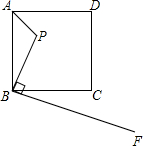 、M、C为顶点的三角形与△ABP相似.(请注意:全等图形是相似图形的特例)
、M、C为顶点的三角形与△ABP相似.(请注意:全等图形是相似图形的特例)
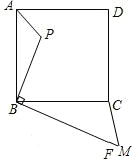 如图,已知点P是边长为4的正方形ABCD内的一点,且PB=3,BF⊥BP,若在射线BF有一点M,使以点B,M,C为顶点的三角形与△ABP相似,那么BM=
如图,已知点P是边长为4的正方形ABCD内的一点,且PB=3,BF⊥BP,若在射线BF有一点M,使以点B,M,C为顶点的三角形与△ABP相似,那么BM=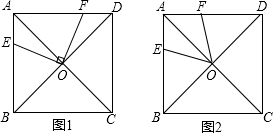
 21、如图,已知点P是边长为4的正方形ABCD内一点,且PB=3,BF⊥BP,垂足是B.
21、如图,已知点P是边长为4的正方形ABCD内一点,且PB=3,BF⊥BP,垂足是B.