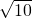题目内容
如图所示，小华同学乘船行驶在湖面上（小华距湖面的高度不计），船行驶到点A处时，小华测得一跨湖大桥桥塔顶端点C的仰角为35°，继续向前行驶60米到达点B处，测得桥塔CE顶端点C在湖中的倒影点D的俯角为45°
，请求出桥塔顶端点C距离湖面的高度CE．
（参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70）
解：在Rt△ACE中，tan35°=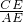
≈0.70，
在Rt△BDE中，tan45°=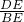
=1，
∵CE=DE，
∴BE=CE，
∴
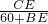=0.70，
解得，CE=140（米）
故桥塔顶端点C距离湖面的高度CE约为140米．
分析：在Rt△ACE中，解直角三角形得出tan35°=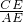≈0.70，在Rt△BDE中得出tan45°=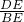=1，根据CE=DE和BE=DE推出BE=CE，代入得出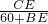=0.70，求出CE即可．
点评：本题考查了解直角三角形的应用，主要考查学生通过解直角三角形求出一些线段的长度，题目比较典型，是一道比较好的题目．
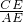≈0.70，在Rt△BDE中，tan45°=
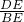=1，∵CE=DE，
∴BE=CE，
∴
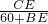=0.70，解得，CE=140（米）
故桥塔顶端点C距离湖面的高度CE约为140米．
分析：在Rt△ACE中，解直角三角形得出tan35°=
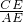≈0.70，在Rt△BDE中得出tan45°=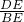=1，根据CE=DE和BE=DE推出BE=CE，代入得出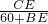=0.70，求出CE即可．点评：本题考查了解直角三角形的应用，主要考查学生通过解直角三角形求出一些线段的长度，题目比较典型，是一道比较好的题目．
练习册系列答案
相关题目
正方形ABCD在坐标系中的位置如图所示，将正方形ABCD绕D点顺时针旋转90°后，B点的坐标为
如图1所示，矩形ABCD的对角线AC、BD交于点O．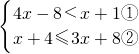
，并把解集在数轴上表示出来．
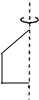下面这个几何体是由哪个图形绕虚线旋转一周形成的
