题目内容
 在直角坐标系中,A(0,4),B(4
在直角坐标系中,A(0,4),B(4| 3 |
(1)当t为何值时,线段CD的长为4;
(2)当线段DE与以点O为圆心,半径为
| 3 |
| 2 |
(3)当t为何值时,以C为圆心、CB为半径的⊙C与(2)中的⊙O相切?
分析:(1)过点C作CF⊥AD于点F,则CF,DF即可利用t表示出来,在Rt△CFD中利用勾股定理即可得到一个关于t的方程,从而求得t的值;
(2)易证四边形ADEC是平行四边形,过点O作OG⊥DE于点G,当线段DE与⊙O相切时,则OG=
,在直角△OEG中,OE可以利用t表示,则OG也可以利用t表示出来,当OG<
时,直线与圆相交,据此即可求得t的范围;
(3)分两圆外切与内切两种情况进行讨论,当外切时,圆心距等于两半径的和,当内切时,圆心距等于圆C的半径减去圆O的半径,列出方程即可求得t的值.
(2)易证四边形ADEC是平行四边形,过点O作OG⊥DE于点G,当线段DE与⊙O相切时,则OG=
| 3 |
| 2 |
| 3 |
| 2 |
(3)分两圆外切与内切两种情况进行讨论,当外切时,圆心距等于两半径的和,当内切时,圆心距等于圆C的半径减去圆O的半径,列出方程即可求得t的值.
解答: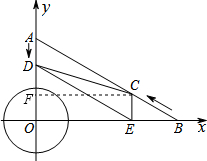 解:(1)过点C作CF⊥AD于点F,
解:(1)过点C作CF⊥AD于点F,
在Rt△AOB中,OA=4,OB=4
,
∴∠ABO=30°,
由题意得:BC=2t,AD=t,
∵CE⊥BO,
∴在Rt△CEB中,CE=t,EB=
t,
∵CF⊥AD,AO⊥BO,
∴四边形CFOE是矩形,
∴OF=CE=t,OE=CF=4
-
t,
在Rt△CFD中,DF2+CF2=CD2,
∴(4-t-t)2+(4
-
t)2=42,即7t2-40t+48=0,
解得:t=
,t=4,
∵0<t<4,
∴当t=
时,线段CD的长是4;
(2)过点O作OG⊥DE于点G(如图2),
∵AD∥CE,AD=CE=t
∴四边形ADEC是平行四边形,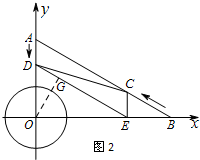
∴DE∥AB
∴∠GEO=30°,
∴OG=
OE=
(4
-
t)
当线段DE与⊙O相切时,则OG=
,
∴当
(4
-
t)<
,且t≥4-
时,线段DE与⊙O有两个公共交点.
∴当 4-
<t≤
时,线段DE与⊙O有两个公共交点;
(3)当⊙C与⊙O外切时,t=
;
当⊙C与⊙O内切时,t=
;
∴当t=
或
秒时,两圆相切.
 解:(1)过点C作CF⊥AD于点F,
解:(1)过点C作CF⊥AD于点F,在Rt△AOB中,OA=4,OB=4
| 3 |
∴∠ABO=30°,
由题意得:BC=2t,AD=t,
∵CE⊥BO,
∴在Rt△CEB中,CE=t,EB=
| 3 |
∵CF⊥AD,AO⊥BO,
∴四边形CFOE是矩形,
∴OF=CE=t,OE=CF=4
| 3 |
| 3 |
在Rt△CFD中,DF2+CF2=CD2,
∴(4-t-t)2+(4
| 3 |
| 3 |
解得:t=
| 12 |
| 7 |
∵0<t<4,
∴当t=
| 12 |
| 7 |
(2)过点O作OG⊥DE于点G(如图2),
∵AD∥CE,AD=CE=t
∴四边形ADEC是平行四边形,

∴DE∥AB
∴∠GEO=30°,
∴OG=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
当线段DE与⊙O相切时,则OG=
| 3 |
| 2 |
∴当
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
∴当 4-
| 3 |
| 5 |
| 2 |
(3)当⊙C与⊙O外切时,t=
| 61 |
| 40 |
当⊙C与⊙O内切时,t=
| 61 |
| 24 |
∴当t=
| 61 |
| 40 |
| 61 |
| 24 |
点评:本题考查了勾股定理以及直线与圆的位置关系,圆与圆的位置关系,正确理解四边形ADEC是平行四边形是关键.

练习册系列答案
相关题目
 在直角坐标系中,将坐标为(5,6),(1,2),(3,2),(3,0),(7,0),(7,2),(9,2),(5,6)的点用线段依此连接起来形成一个图案.
在直角坐标系中,将坐标为(5,6),(1,2),(3,2),(3,0),(7,0),(7,2),(9,2),(5,6)的点用线段依此连接起来形成一个图案. 如图,△ABC在直角坐标系中,
如图,△ABC在直角坐标系中,