题目内容
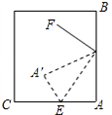
23、如图，斜折一页书的一角，使点A落在同一书页的A′处，DE为折痕，作DF平分∠A′DB，试猜想∠FDE等于多少度，并说明理由．分析：根据翻折变换的性质可得到∠ADE=∠A′DE，再根据DF平分∠A′DB可得到∠A′DF=∠BDF，由平角的性质即可得出结论．
解答：解：猜想：∠FDE等于90°．
∵斜折一页书的一角，使点A落在同一书页的A′处，DE为折痕，
∴∠ADE=∠A′DE，
又∵DF平分∠A′DB，
∴∠A′DF=∠BDF，
而∠ADA′+∠BDA′=180°，则∠FDE=90°．
故答案为：90°．
∵斜折一页书的一角，使点A落在同一书页的A′处，DE为折痕，
∴∠ADE=∠A′DE，
又∵DF平分∠A′DB，
∴∠A′DF=∠BDF，
而∠ADA′+∠BDA′=180°，则∠FDE=90°．
故答案为：90°．
点评：本题考查的是图形翻折变换的性质及角平分线的性质，熟知图形翻折变换的性质是解答此题的关键．
练习册系列答案
相关题目
如图所示，斜折一页书的一角，使点A落在同一书页内的F处，DE为折痕，作DG平分∠BDF，试猜想∠EDG等于多少度，并说明理由．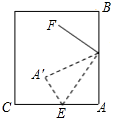
如图，斜折一页书的一角，使点A落在同一书页的A′处，DE为折痕，作DF平分∠A′DB，试猜想∠FDE等于多少度，并说明理由．
