Question

【题目】在△ABC中，CD⊥AB于点D，DA=DC=4，DB=2，AF⊥BC于点F，交DC于点E．

（1）求线段AE的长；

（2）若点G是AC的中点，点M是线段CD上一动点，连结GM，过点G作GN⊥GM交直线AB于点N，记△CGM的面积为S1，△AGN的面积为S2．在点M的运动过程中，试探究：S1与S2的数量关系

Answer 1

【答案】（1）；（2）S1+S2=4，见解析

【解析】

（1）先证明△ADE≌△CDB，得到DE=DB=2，在Rt△ADE中，利用勾股定理求出AE．

（2）过点G作CD，DA的垂直线，垂足分别为P，Q，证明△MGP≌△NGQ，所以S1+S2=S△AGQ+S△CGP= S△ACD-S四边形GQDP，即可求解．

（1）在△ABC中，CD⊥AB，AF⊥BC

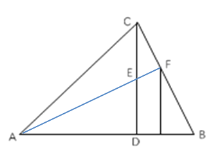
∴∠ADC=∠AFB=90°

∵∠AED=∠CEF

∴∠EAD=∠BCD

在△ADE和△CDB中

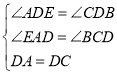
∴△ADE≌△CDB

∴DE=DB=2

∴AE=

（2）在△ABC中，CD⊥AB，DA=DC=4，

点G是AC的中点

过点G作CD，DA的垂直线，垂足分别为P，Q．

则，GP=GQ=DA=2

∠PGQ=90°=∠GQN=∠GPM

∵GN⊥GM

∴∠MGN=90°

∴∠MGP=∠NGQ

∴△MGP≌△NGQ

S1+S2=S△AGQ+S△CGP= S△ACD-S四边形GQDP=

故答案为：4