题目内容
【题目】(本题满分10分)如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
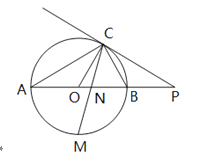
(1)求证:PC是⊙O的切线;
(2)求证:BC=![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN·MC的值.
【答案】
(1)PC是⊙O的切线,证明略。
(2)BC=![]() AB,证明略。
AB,证明略。
(3)MC·MN=BM2=8
【解析】(本题满分10分)
解:(1)∵OA=OC,∴∠A=∠ACO
∵∠COB=2∠A ,∠COB=2∠PCB
∴∠A=∠ACO=∠PCB ……………………………………………………1分
∵AB是⊙O的直径
∴∠ACO+∠OCB=90° …………………………………………………2分
∴∠PCB+∠OCB=90°,即OC⊥CP …………………………………………3分
∵OC是⊙O的半径
∴PC是⊙O的切线 …………………………………………………4分
(2)∵PC=AC ∴∠A=∠P
∴∠A=∠ACO=∠PCB=∠P
∵∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB
∴∠CBO=∠COB ……………………………………………5分
∴BC=OC
∴BC=![]() AB ………………………………………………………6分
AB ………………………………………………………6分
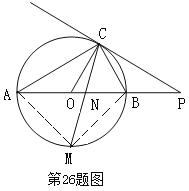
(3)连接MA,MB
∵点M是弧AB的中点
∴弧AM=弧BM ∴∠ACM=∠BCM ………7分
∵∠ACM=∠ABM ∴∠BCM=∠ABM
∵∠BMC=∠BMN
∴△MBN∽△MCB
∴![]()
∴BM2=MC·MN ……………………8分
∵AB是⊙O的直径,弧AM=弧BM
∴∠AMB=90°,AM=BM
∵AB=4 ∴BM=![]() ………………………………………………………9分
………………………………………………………9分
∴MC·MN=BM2=8 ……………………………………………………10分

【题目】某校为进行危房改造,政府最近将在某校搭建板房,从某厂调拔了用于搭建板房的板材5600m3和铝材2210m3 , 计划用这些材料在某校搭建甲、乙两种规格的板房共100间.若搭建一间甲型 板房或一间乙型板房所需板材和铝材的数量如表所示:
板房规格 | 板材数量(m3) | 铝材数量(m3) |
甲型 | 40 | 30 |
乙型 | 60 | 20 |
请你根据以上信息,设计出甲、乙两种板房的搭建方案.