题目内容
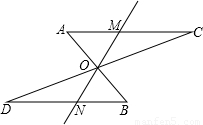
（2007•宜宾）如图，将△BOD绕点O旋转180°后得到△AOC，再过点O任意画一条与AC、BD都相交的直线MN，交点分别为M和N．试问：线段OM=ON成立吗？若成立，请进行证明；若不成立，请说明理由．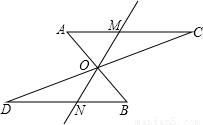
【答案】分析：根据旋转的意义可证△AOM≌△BON或△COM≌△DON，即证OM=ON．
解答：解：线段OM=ON成立，
证明：∵OA=OB，
∠OAC=∠OBD，
∠AOM=∠BON，
∴△AOM≌△BON，
∴OM=ON．
点评：本题考查了旋转的意义，和全等三角形的判定，是一道基础题．
解答：解：线段OM=ON成立，
证明：∵OA=OB，
∠OAC=∠OBD，
∠AOM=∠BON，
∴△AOM≌△BON，
∴OM=ON．
点评：本题考查了旋转的意义，和全等三角形的判定，是一道基础题．
练习册系列答案
相关题目
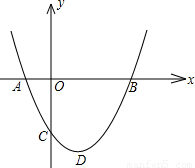
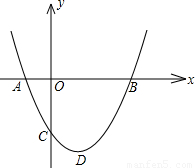
时，△ABD是等腰直角三角形；⑤使△ACB为等腰三角形的a的值可以有三个．那么，其中正确的结论是 ．
时，△ABD是等腰直角三角形；⑤使△ACB为等腰三角形的a的值可以有三个．那么，其中正确的结论是 ．
时，△ABD是等腰直角三角形；⑤使△ACB为等腰三角形的a的值可以有三个．那么，其中正确的结论是 ．