题目内容
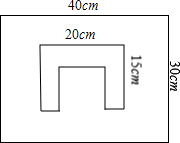 已知一块长方形木板长40cm,宽30cm,在木板中间挖去一个底边长为20cm,高为15cm且宽度相同的U形孔(如示意图),已知剩下的木板面积是原来面积的
已知一块长方形木板长40cm,宽30cm,在木板中间挖去一个底边长为20cm,高为15cm且宽度相同的U形孔(如示意图),已知剩下的木板面积是原来面积的| 5 | 6 |
分析:本题可设U形孔的宽为xcm,则U形孔的面积为[20x+2x(15-x)]cm2,进而可列出方程,求出答案.
解答:解:根据题意,设U形孔的宽为xcm,根据题意得,(1分)
40×30×(1-
)=20x+2x(15-x),(3分)
即x2-25x+100=0.
解得x1=5,x2=20(此时2x=40,占去了木板的全部宽度,不合题意舍去),(1分)
答:宽度为5cm.
40×30×(1-
| 5 |
| 6 |
即x2-25x+100=0.
解得x1=5,x2=20(此时2x=40,占去了木板的全部宽度,不合题意舍去),(1分)
答:宽度为5cm.
点评:这类题目体现了数形结合的思想,需仔细分析图形,利用方程来解决问题,另外还要注意解的合理性,从而确定取舍.

练习册系列答案
相关题目
 已知一块长方形木板长40cm,宽30cm,在木板中间挖去一个底边长为20cm,高为15cm且宽度相同的U形孔(如示意图),已知剩下的木板面积是原来面积的
已知一块长方形木板长40cm,宽30cm,在木板中间挖去一个底边长为20cm,高为15cm且宽度相同的U形孔(如示意图),已知剩下的木板面积是原来面积的 ,求挖去的U形孔的宽度.
,求挖去的U形孔的宽度. ,求挖去的U形孔的宽度.
,求挖去的U形孔的宽度.
 ,求挖去的U形孔的宽度.
,求挖去的U形孔的宽度.
 ,求挖去的U形孔的宽度.
,求挖去的U形孔的宽度.