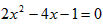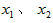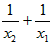Question

设a、b是一元二次方程x²-2x-1=0的两个根，且2a（b²-3b-1）+m=3，则m的值为

1. A.
   -1
2. B.
   1
3. C.
   2
4. D.
   5

Answer 1

B
分析：根据根与系数的关系先求出a+b=2，ab=-1，然后把2a（b²-3b-1）+m=3，变形后代入即可求解．
解答：∵a、b是一元二次方程x²-2x-1=0的两个根，
∴a+b=2，ab=-1，
∴2a（b²-3b-1）+m=2a（b²-3b+ab）+m
=2ab（b-3+a）+m
=-2（2-3）+m
=2+m=3，∴m=1，
故选B．
点评：本题考查了根与系数的关系及一元二次方程的解，属于基础题，关键是掌握根与系数的关系．